Introduction
The aim of this post is to give the updated baseline portfolio weights of the Polar Star Diversified Commodity Fund for the second quarter of 2020. We employ the Black-Litterman methodology to tilt the allocations slighlty toward the underlying fund the greater return expectations and confidence. For more details on the process please see this link as well as other referenes therein.
Baseline Weights
To obtain baseline weights, we perform a risk-adjusted return portfolio optimisation with the returns stream of the three underlying funds
- Polar Star Ltd
- Polar Star Specturm
- Polar Star Quantitataive
We use a training period of 12 months from which we determine the optimal portfolio in the following month. In previous calculations we used 12 months of returns with an expanding window to determine the optimal wights, here we use a 12 month rolling window. The evolution of the optimal weights is shown in the plot below for three different optimisation schemes. These are just numerical method used to determine the optimal weights. Notice that we have reduced the range of returns to start from 2015, this is done to place a greater emphasis on returns closer to the current regime.
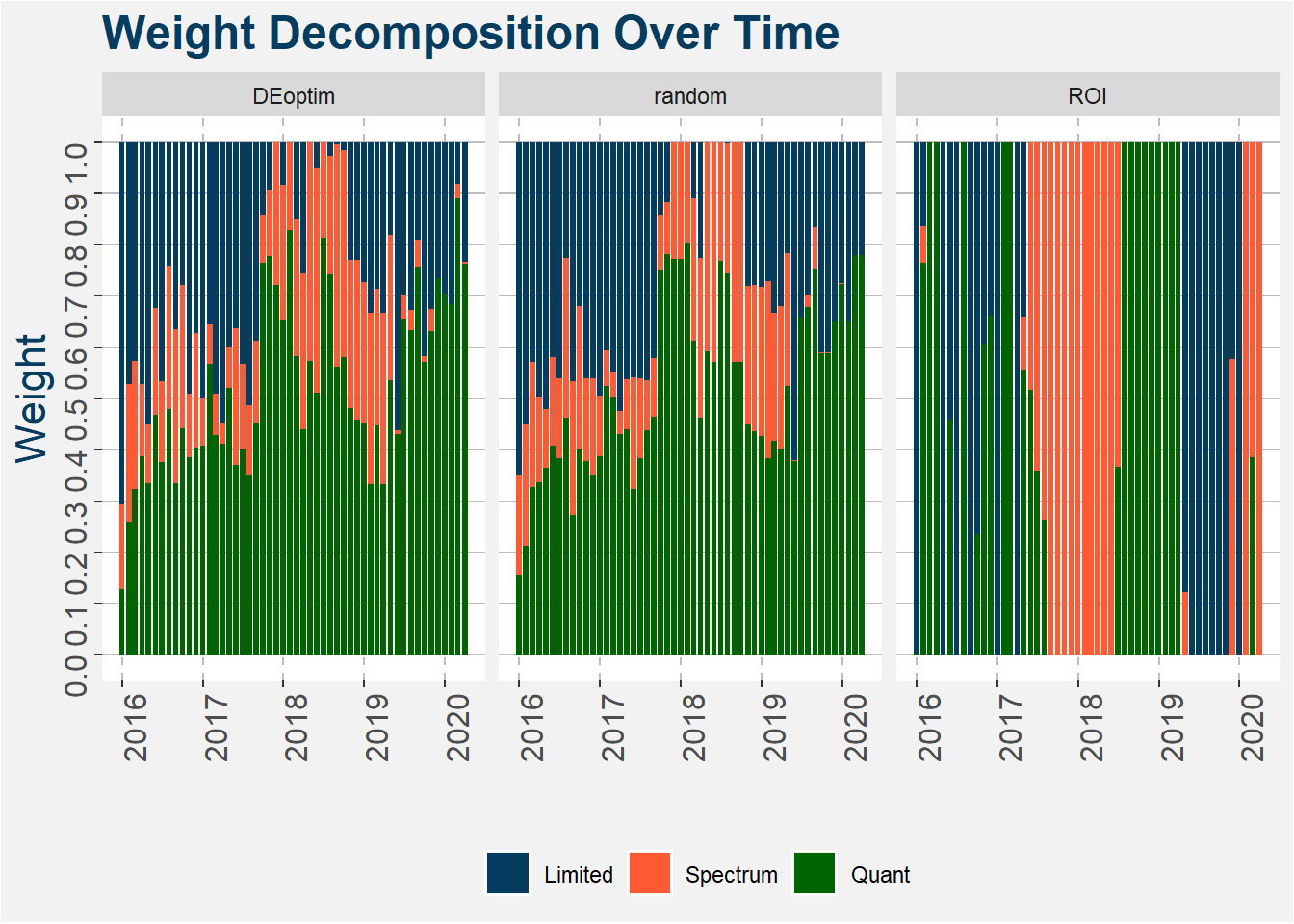
As baseline weights we take the average of the optimised weights given by the table below. Here each columns from the ROI method as the baseline weights.
| fund | Average | DEoptim | ROI | random |
|---|---|---|---|---|
| Limited | 0.31 | 0.291 | 0.324 | 0.304 |
| Spectrum | 0.22 | 0.184 | 0.307 | 0.177 |
| Quant | 0.47 | 0.525 | 0.369 | 0.519 |
Weight Change vs Confidence
If you are interested in the mathematical details of the view and confidence extension to the Black-Litterman model by Idzorek please follow the link. We will not go through any of the details here. Instead, we will investigate the effect of changing confidence in the positive return forecast.
| return | confidence | fund |
|---|---|---|
| 0.03 | 0.65 | Limited |
| 0.05 | 0.70 | Spectrum |
| 0.03 | 0.55 | Quant |
We fix the confidences of Polar Star Quantitative and Polar Star Limited to their values as indicated in the table above. Next, we vary the confidence of the expected return on Polar Star Spectrum from 1% to 100% and calculate how the weight changes between the three funds. The results are shown in the table below. The vertical black line shows the baseline confidence as given in the table above. The weights indicated next to the vertical line show the weights at the baseline numbers. Notice that the allocation to Polar Star Spectrum increases as the confidence in the expected return increases.
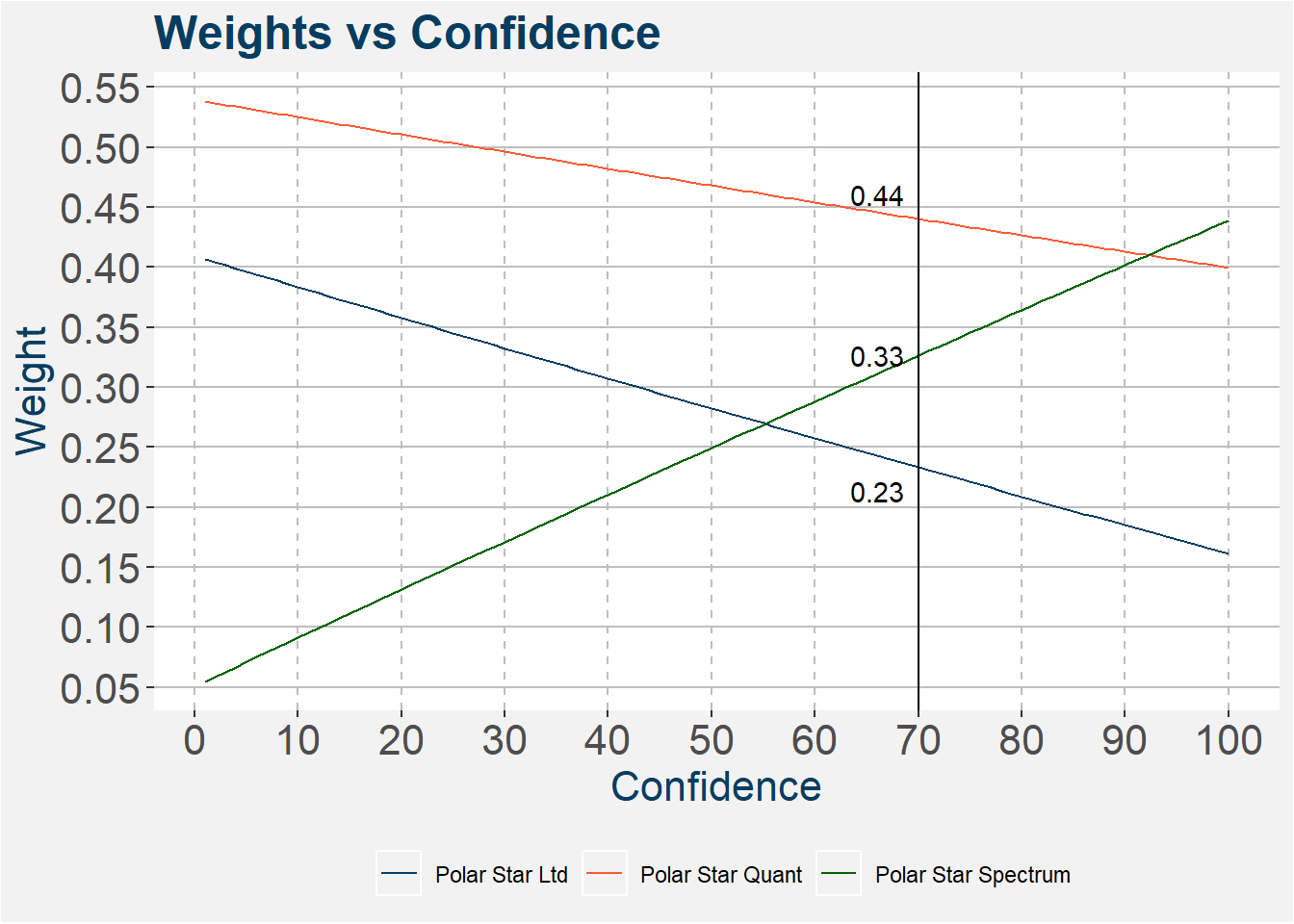
The table below shows the weights after tilting the allocations slighlty according to the outline above.
| Fund | Confidence | Weight |
|---|---|---|
| Polar Star Ltd | 70 | 0.233 |
| Polar Star Spectrum | 70 | 0.326 |
| Polar Star Quant | 70 | 0.440 |
Weight Change vs Return Forecast
Similar to the case above we fix the return forecasts of Polar Star Quantitative and Polar Star Limited and let the return forecast of Polar Star Spectrum vary from 0 through 10%. Notice that the numbers shown in the image below take the quarterly forecasts and generate a monthly aggregate number from it. Notice that as the reutrn forecast increases so the wieght allocated to Polar Star Spectrum increases.
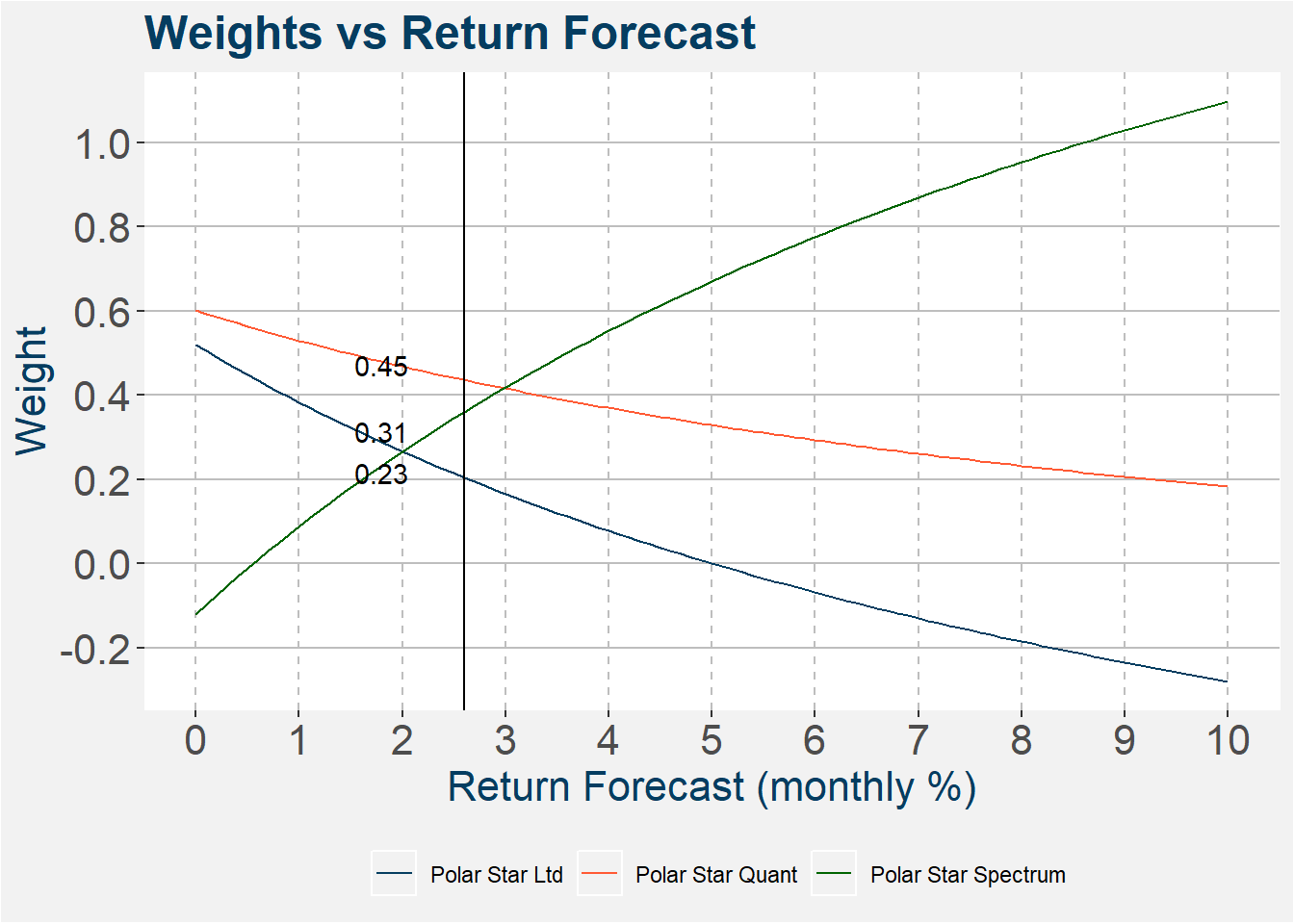
The table below shows the weights after tilting the allocations slighlty according to the outline above.
| Fund | Return Forecast (monthly) | Weight |
|---|---|---|
| Polar Star Ltd | 0.023 | 0.235 |
| Polar Star Spectrum | 0.023 | 0.314 |
| Polar Star Quant | 0.023 | 0.452 |
Remarks
The final return projections and associated confidence levels have to be finilised by the portfolio managers of each of the underlying funds.