Introduction
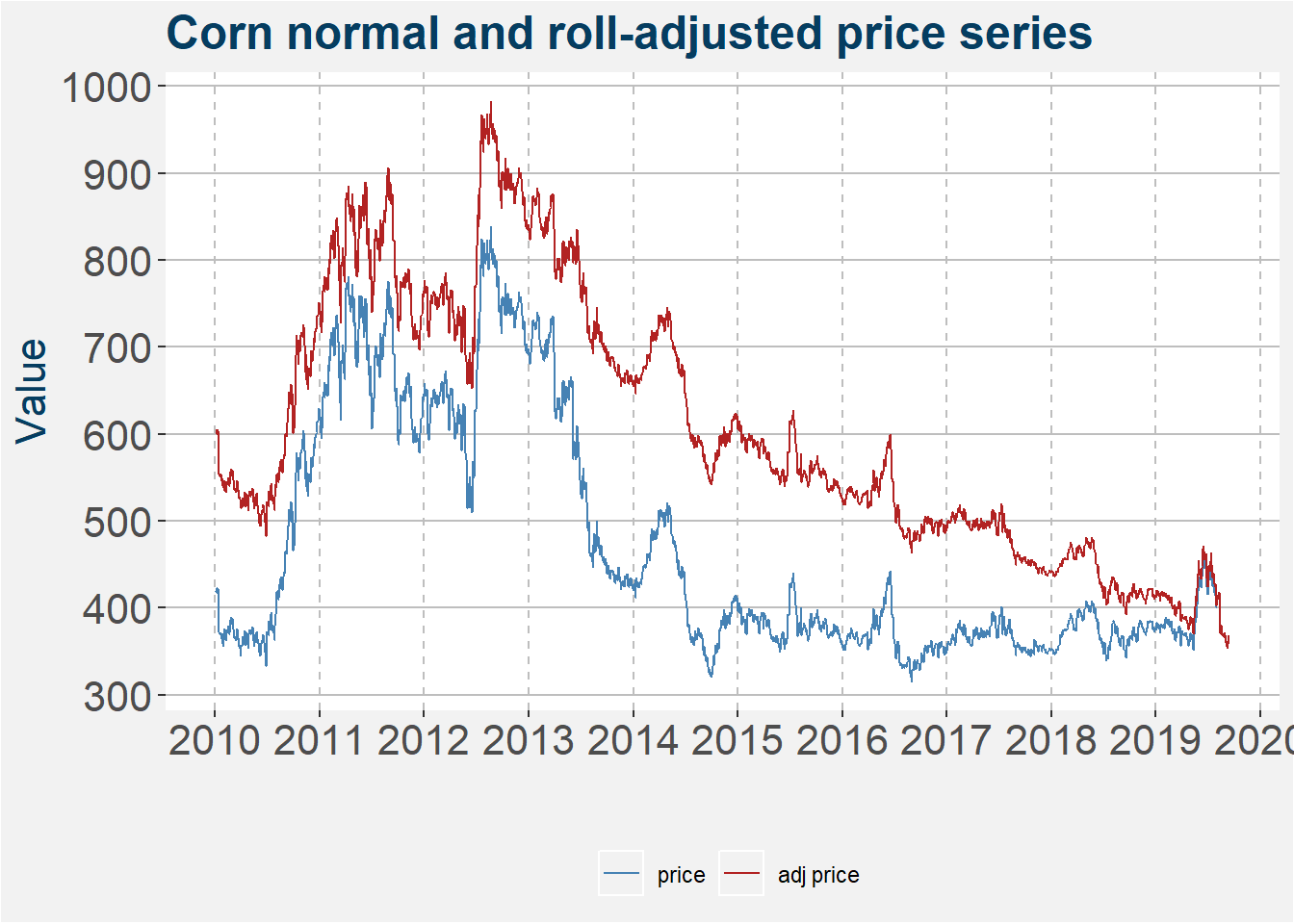
The aim of this write-up is to explore the price evolution after different thresholds of net managed money have been crossed. The COT data containing the net managed money numbers have been collected using Bloomberg. Note that the dates assocated with the bloomberg data is not correct. Generally, the data is for the positions on a Tuesday, but only reported on a Friday. The first time the market has access to this data, most of the time, is on a Friday. We changed the dates associated with the COT data by three days to account for this mismatch. In the remainder of the write-up the analysis is performed on roll-adjusted price series of the different commodities. The plot below shows the normal and roll-adjusted price series for corn since 2010. Notice the general downward drift after the peak in during the 2012/13 season.
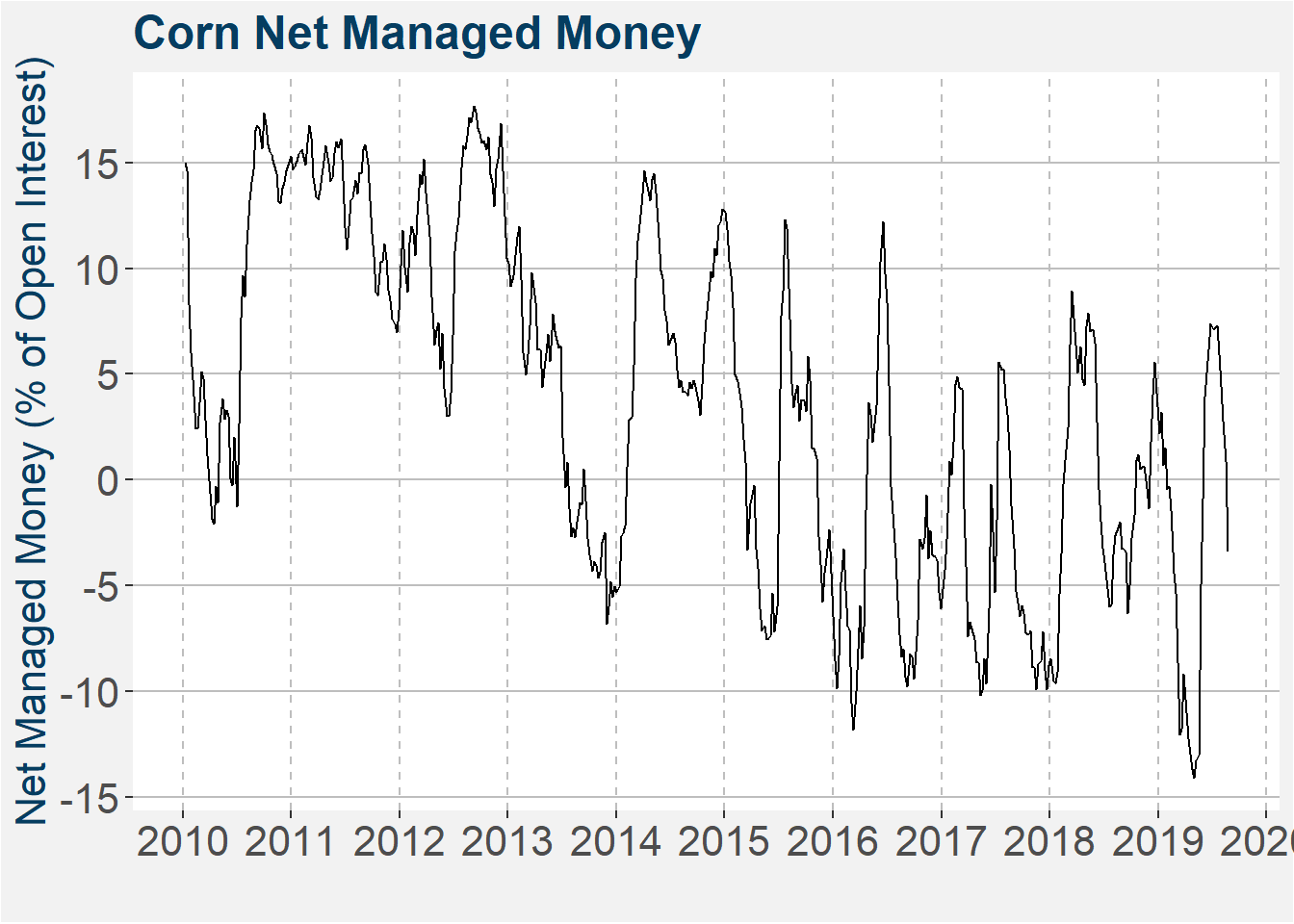
The plot below shows the evolution of the Corn net managed money position expressed as a percentage of open interest since 2010. In the following we will look at the net managed money is two ways, decile buckets and directional threshold crosses.
Decile Buckets
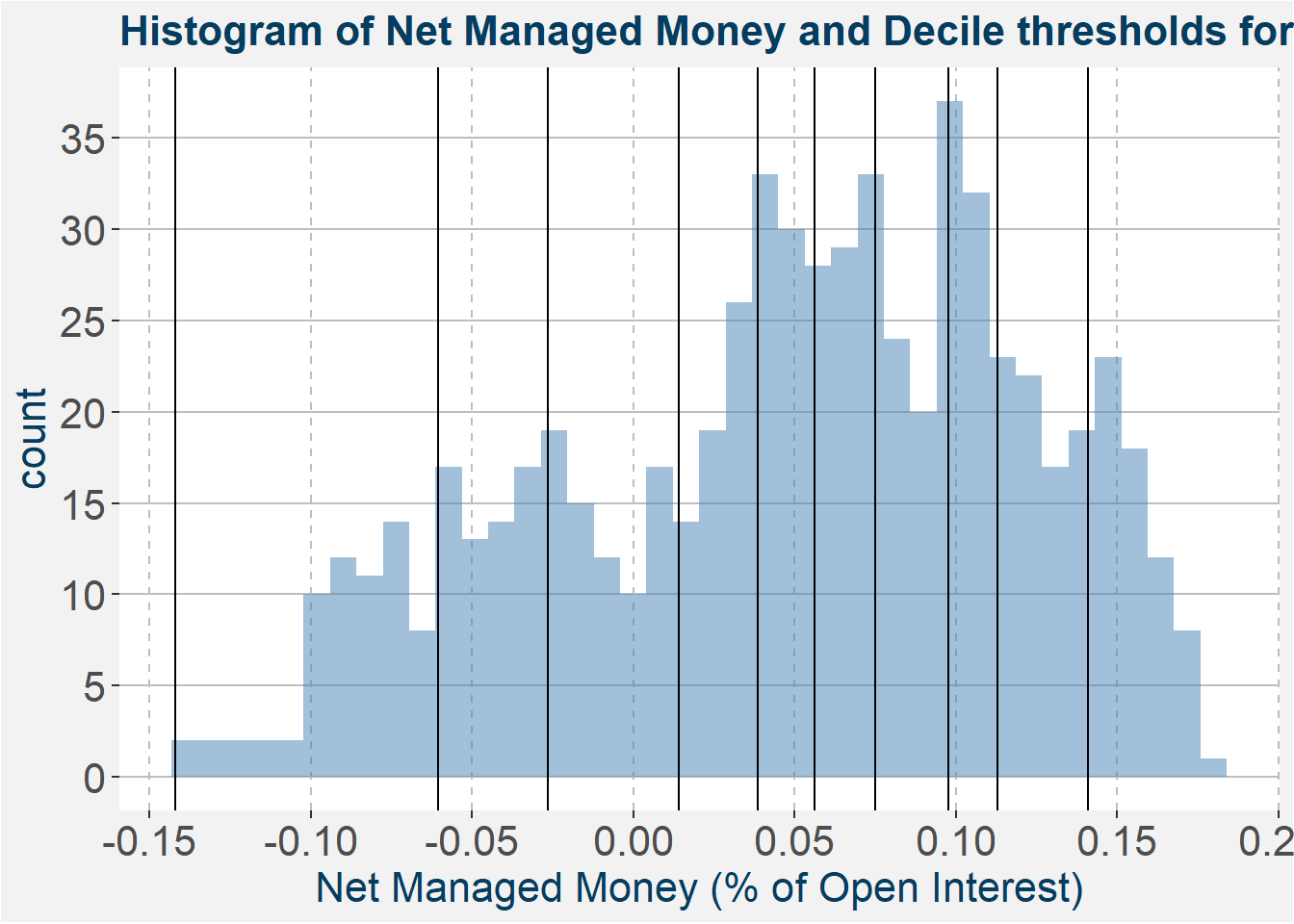
The plot below shows the distribution of Net Managed Money as a percentage of open interest for Corn. Each vertical line shows the start of a decile bucket. Each decile contains 10 percent of the data in the sample. In the next plot we show the aggragated price evolution when the Net Manged Money lies within each of the decile buckets.
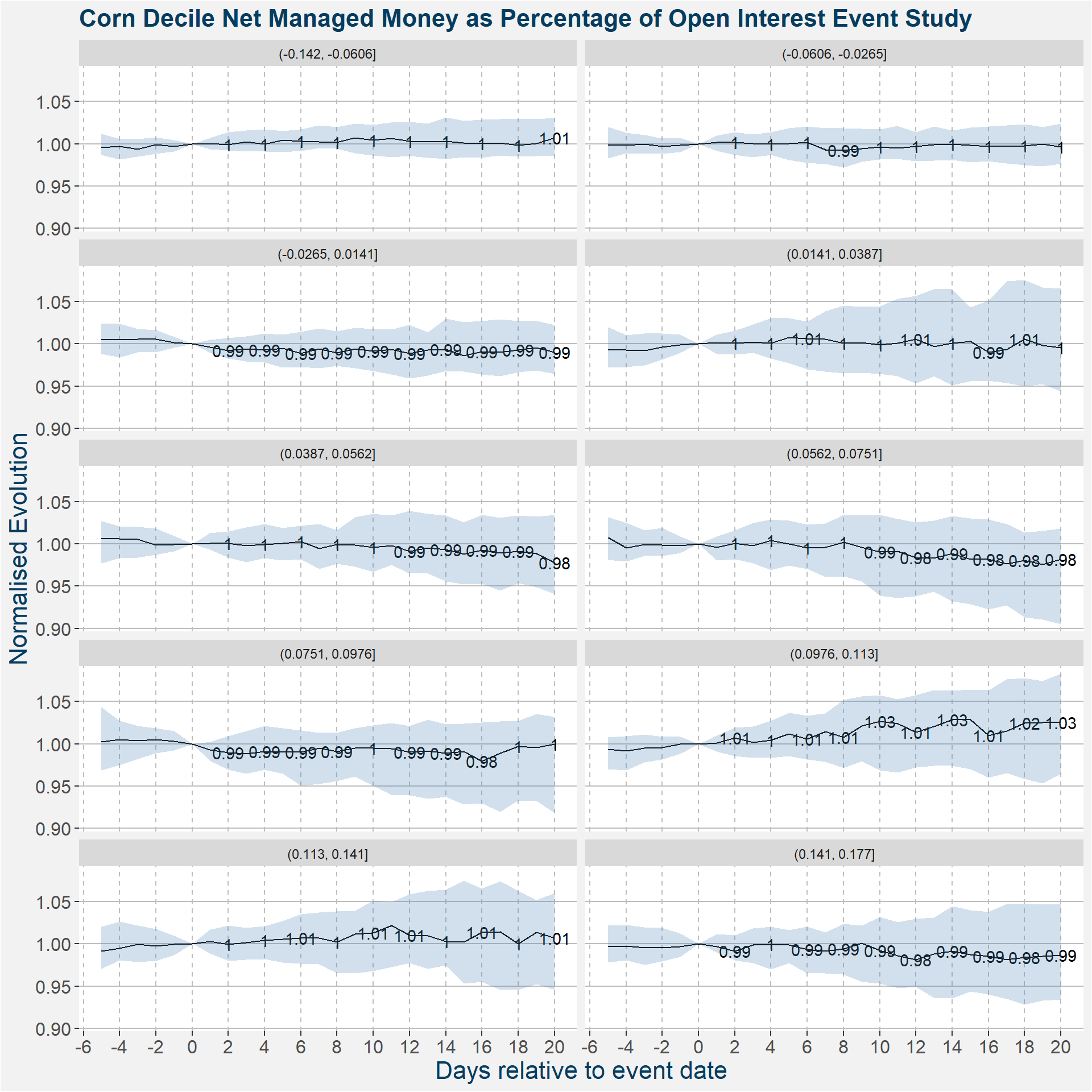
Each of the ten plots below show the 25th to 75th percentile of the return after the event represented by the blue shaded region. The median is given by the superimposed black line. As an example, let us consider the top left facet with the Net Managed Money bucket of (-0.142, -0.0606]. This corresponds to the most negative decile in the distribution of Net Managed Money. In this case the evolution is more or less flat after the event has been triggered. If we consider the opposite side of the Net Managed Money spectrum, the bottom right facet, we see the aggregated evolution after the events when the Net Managed Money is in the rightmost part of the distribution. Here we see that the meadian lies two percent under the starting value ten days after the event. Hence, if the market is positioned sufficiently long we see a statistically significant decrease in price following the publicaiton of the long Net Managed Money position.
The table below shows the number of entries in each of the buckets. Since we are using deciles to group the data we should expect to see similar counts in each of the buckets. Recall that the COT data is published with a weekly frequency, hence all the buckets contain well beyond a year’s worth of data.
| bucket | count |
|---|---|
| (-0.142, -0.0606] | 67 |
| (-0.0606, -0.0265] | 67 |
| (-0.0265, 0.0141] | 67 |
| (0.0141, 0.0387] | 66 |
| (0.0387, 0.0562] | 67 |
| (0.0562, 0.0751] | 67 |
| (0.0751, 0.0976] | 66 |
| (0.0976, 0.113] | 67 |
| (0.113, 0.141] | 67 |
| (0.141, 0.177] | 66 |
Directional Buckets
In this section we are more interested in the direction in which the Net Managed Money expressed as a percentage of open interest changes with respect to some threshold value. Note that there are two posiible ways a threshold value can be crossed, we can either increase or decrease beyond the theshold value. For example if the threshold value is 0.1 and we see a change of 0.08 to 0.12 we have increased beyond the threshold value. Similary, if the theshold value is -0.04 and we see a change from 0 to -0.5 we have decreased beyond the threshold. These events are identified according to the threshold and direction in which it was crossed. In the plots below we show the aggregated data for Corn with negative thresholds.
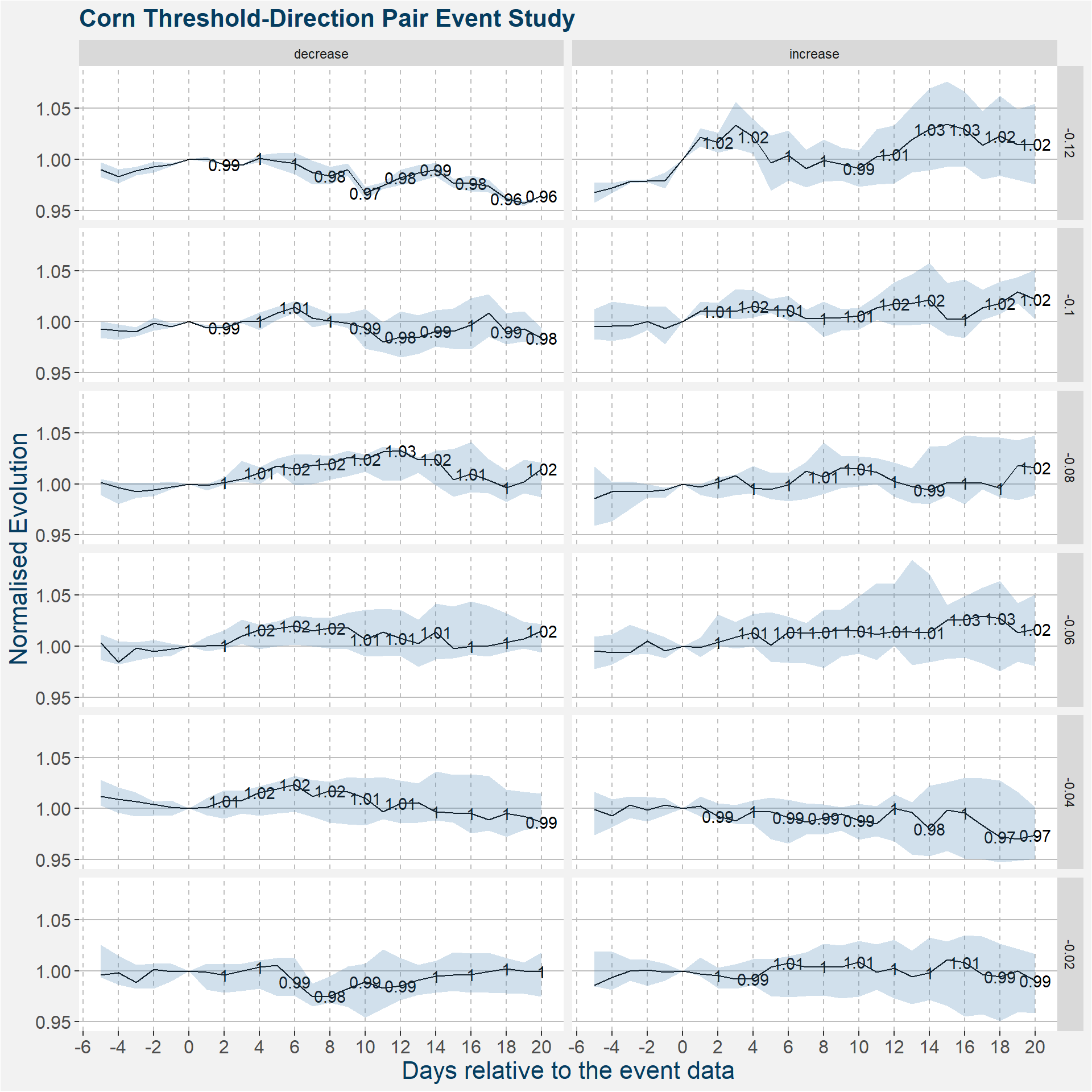
The table below shows the number of counts for each threshold and direction. Note that the lower the threshold the less observation we have and the less statistically signigicant the results become. For the lowest threshold values we only have two observation for each of the directions. This is not nearly enought to draw any statistical relationship from.
| threshold | decrease | increase |
|---|---|---|
| -0.12 | 2 | 2 |
| -0.10 | 4 | 4 |
| -0.08 | 9 | 9 |
| -0.06 | 13 | 13 |
| -0.04 | 15 | 15 |
| -0.02 | 15 | 14 |
Results for W
Decile
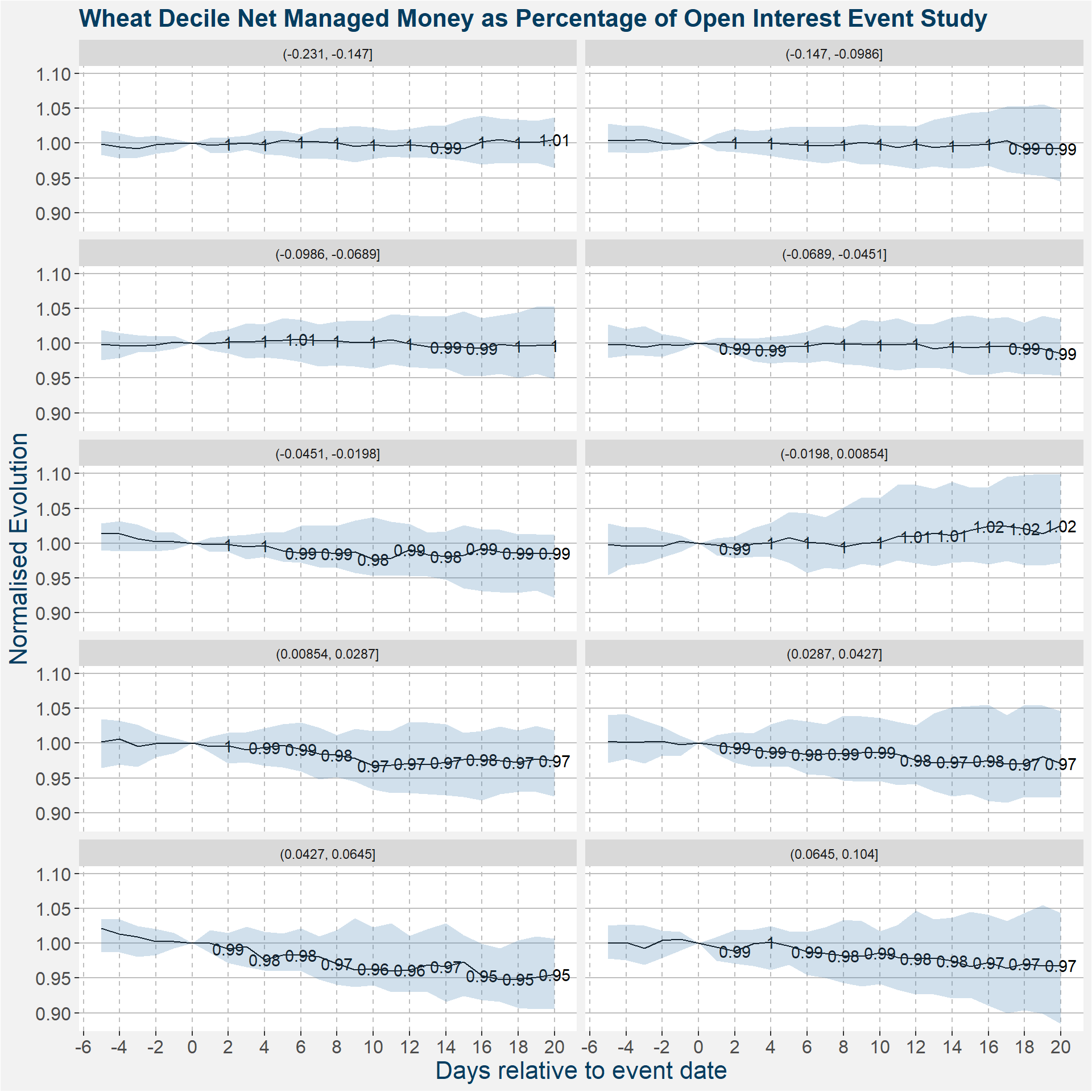
| bucket | count |
|---|---|
| (-0.231, -0.147] | 67 |
| (-0.147, -0.0986] | 67 |
| (-0.0986, -0.0689] | 67 |
| (-0.0689, -0.0451] | 66 |
| (-0.0451, -0.0198] | 67 |
| (-0.0198, 0.00854] | 67 |
| (0.00854, 0.0287] | 66 |
| (0.0287, 0.0427] | 67 |
| (0.0427, 0.0645] | 67 |
| (0.0645, 0.104] | 66 |
Directional
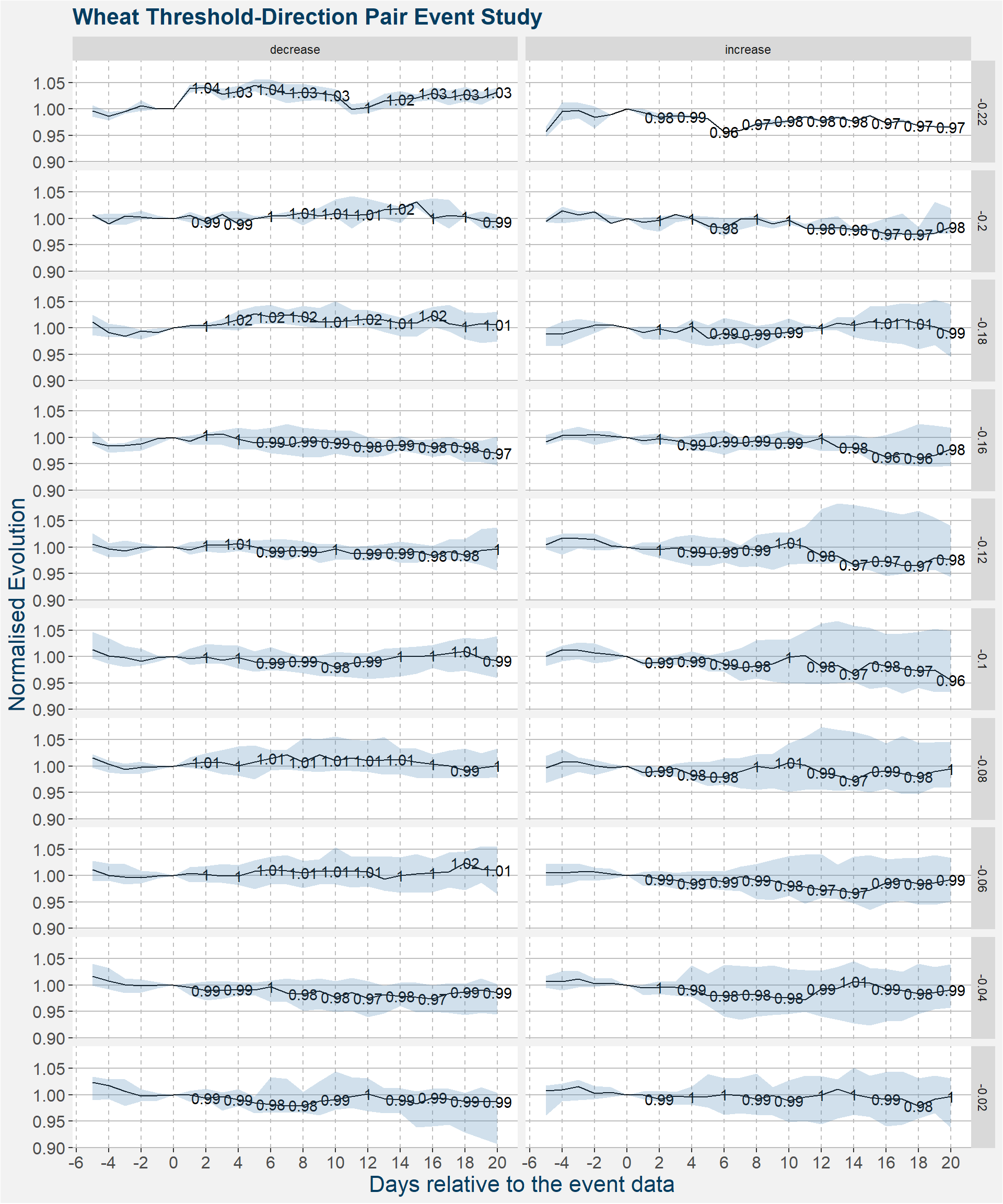
| threshold | decrease | increase |
|---|---|---|
| -0.22 | 2 | 2 |
| -0.20 | 5 | 5 |
| -0.18 | 10 | 10 |
| -0.16 | 11 | 11 |
| -0.12 | 12 | 12 |
| -0.10 | 15 | 15 |
| -0.08 | 19 | 19 |
| -0.06 | 30 | 30 |
| -0.04 | 20 | 20 |
| -0.02 | 21 | 21 |
Results for SM
Decile
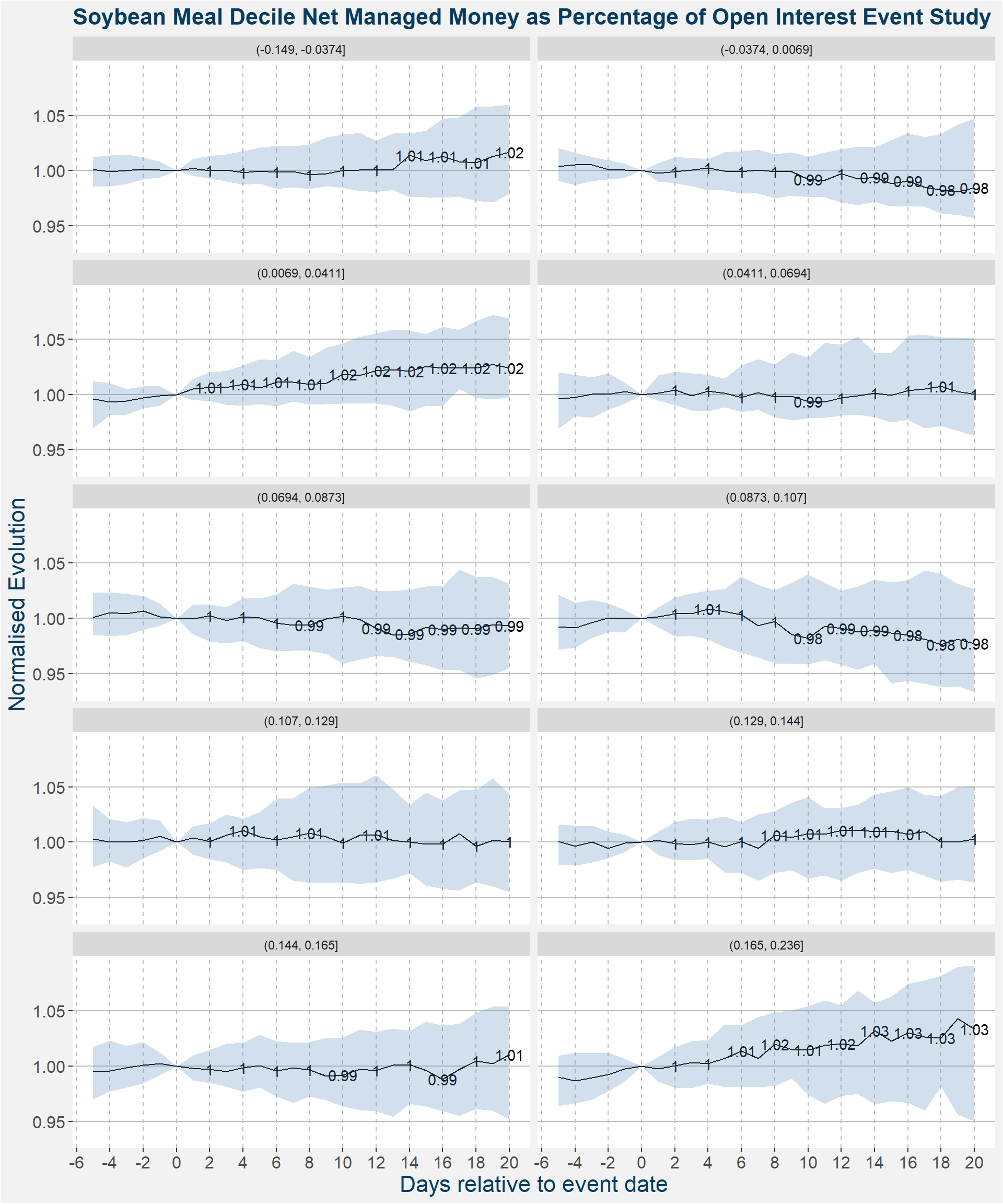
| bucket | count |
|---|---|
| (-0.149, -0.0374] | 67 |
| (-0.0374, 0.0069] | 67 |
| (0.0069, 0.0411] | 67 |
| (0.0411, 0.0694] | 66 |
| (0.0694, 0.0873] | 67 |
| (0.0873, 0.107] | 67 |
| (0.107, 0.129] | 66 |
| (0.129, 0.144] | 67 |
| (0.144, 0.165] | 67 |
| (0.165, 0.236] | 66 |
Directional
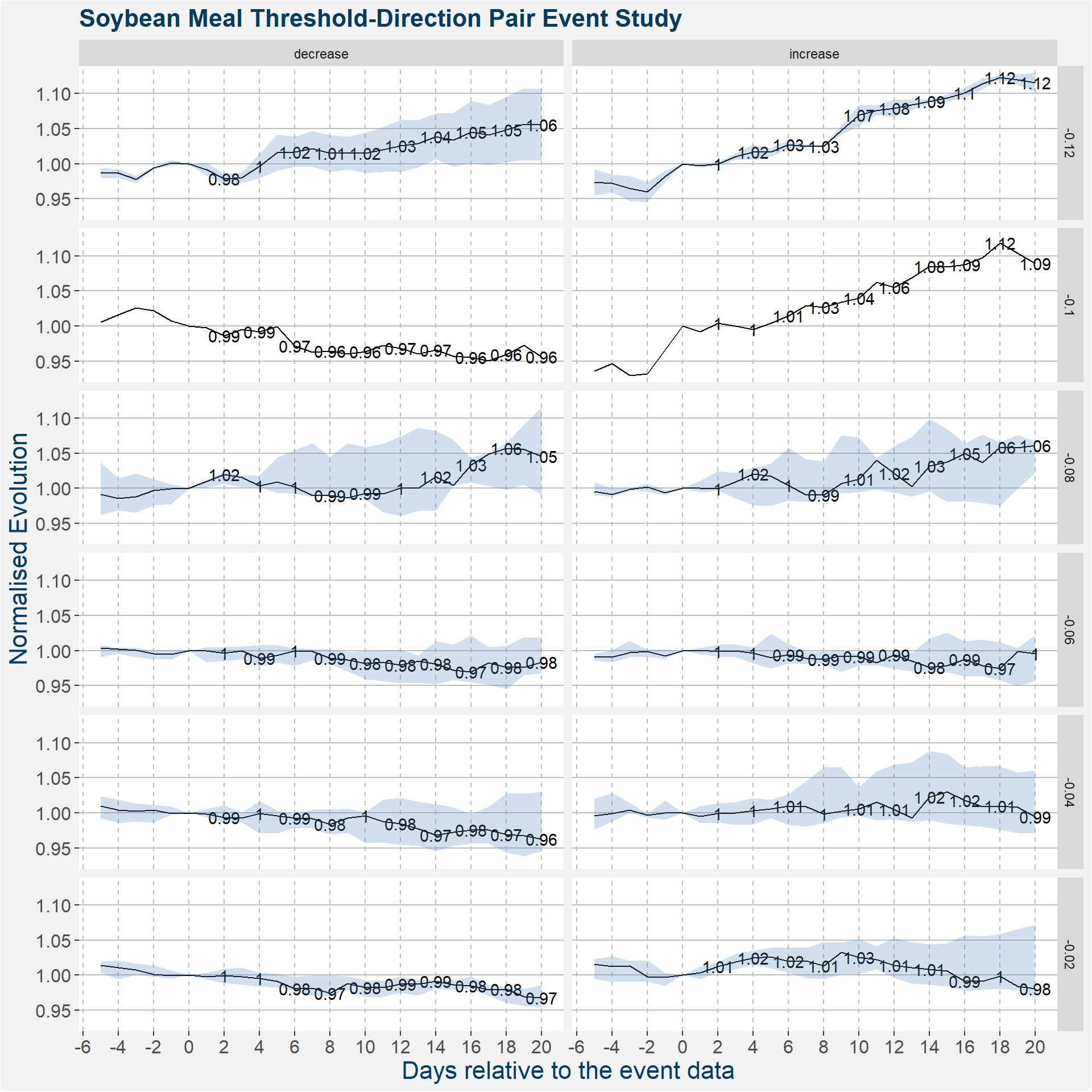
| threshold | decrease | increase |
|---|---|---|
| -0.12 | 2 | 2 |
| -0.10 | 1 | 1 |
| -0.08 | 5 | 5 |
| -0.06 | 9 | 9 |
| -0.04 | 10 | 9 |
| -0.02 | 8 | 8 |
Academic Literature
An article that always get cited when you see work on COT data and hedging pressure is
Their basic idea is to use a single and double sorted portfolio where they
- buy the contracts for which hedgers are the shortest and/or speculators are the longest and
- sell the contracts for which hedgers are the longest and speculators are the shortest
This can be seen as following the managed money rather than betting against it. The reported results are also pretty good with Sharpe ratios in the range 0.27 to 0.93 with an average of 0.53.
Remarks
- Extreme Net Managed Money positions by definition will not have statistical significance because the sample size is just way too small.
- Using a decile bucketing methodology we can increase the sample sizes to look for tradeable opportunities at the extremes
- The threshold-direction pairs make more sense because it captures the direction in which the Net Managed Money is moving. However, here the sample sizes are small and clear results are difficult to derive.
- The academic approad is to follow the Managed Money.