1 Introduction
We get asked often is if we have a long-only commodities product or if we can give investors access to long-only commodities exposure. In this document, we show why this is, in general, not a good idea. We do this by studying the Bloomberg Commodities index which is one of the long-only commodity benchmarks. We introduce the concepts of backwardation and contango and show how the curve structure affects the profits of a long-only portfolio.
We create a proxy index roughly based on the Bloomberg Commodity Index with weightings equal to the average of all available weight data and follow the rolling methodology outlined by the index. We show the effects of backwardation and contango on the performance of the long-only index and create a hybrid index that can take both long and short exposure in the underlying commodities depending on the curve structure during rolling periods.
We show how a trend following strategy, that only includes the BCOM commodities and expiries, outperforms all the previous index constructions. We compare the performance attributions of the different commodities during periods of backwardation and contango. Finally, we highlight the added benefit of additional diversification by extending the allowed universe of investible commodities.
2 Bloomberg Commodities Index
The Bloomberg Commodities Index consists of long positions in the most liquid US dollar-denominated commodities. The weights only change on a year to year basis. Members sometimes change according to their mandate but stay roughly the same for the most part. The graphs below show the value of the BCOM index since January 1990. The horizontal red line compares the last available data with historical numbers. Notice that the current level of the BCOM Index is similar to those experienced during 1992 and 2016.
Unfortunately Bloomberg only provides weight data from 2015 onwards. The plot below shows the weights for every commodity included in the index by year. Notice the large allocations to gold and the energies.
3 Reconstructing Bloomberg Commodities Index
In this section, we simplify the weighting scheme of the standard BCOM Index. We use the simplified weights to reconstruct the BCOM Index in a modified version. The performance of the reconstructed index can be explained by studying the curve structures of the commodities making up the index. The continuous roll adjusted time series gives a good visual aid in describing the effect of contango and backwardation for each of the commodities. We create three models to compare with the original reconstructed index,
- long-only portfolio with commodities in backwardation
- Short only portfolio with commodities in contango
- Combo portfolio with long and short exposure to commodities in backwardation and contango respectively
3.1 Simplifying the weights
Notice that the BCOM Index is constructed in such a way that it does not take trading cost or slippage into account. In the following, we try to replicate the BCOM Index on a more realistic basis. Here we include trading costs of USD 5 per contract as well as a tick’s worth of slippage for each trade. To simplify the weights per commodity we take the average of all available weight data for each of the commodities and normalise the results. The weights we use in reconstructing the index are shown in the plot below. Here it is easier to see that the index is overweight energies and gold.
The main reason behind reconstructing the index and performing a more realistic backtest is that it enables us to look at the performance during certain curve shapes.
3.2 Curve Shape
Commodity traders use the nomenclature of backwardation and contango when referring to the shape of a futures curve. Backwardation refers to the state where further dated futures contracts are priced lower than the near-dated or front contract. Contango, is exactly the opposite and refers to the state where the further-dated part of the curve is priced higher than the front month.
In general the shape of the futures curve is determined by the underlying supply and demand dynamics of the commodity. When the supply of a commodity is high, the stocks need to be carried along the futures curve. Physically, this amounts to storing the commodity in a silo or wareshouse. The greater the quantity of the commodity that needs to be stored, the higher the cost. This cost is carried along the futures curve and forces the later dated futures higher. Conversely, notice that a large supply of a commodity implies a lower price according to standard supply and demand dynamics. The naive investor might argue that the price is cheap compared to historical values and it is a good idea to have long exposure. If this investor want to keep this long exposure he needs to roll his position up the contango curve before his contract expires. Heuristically, this implies that he has to sell a cheap future and buy a more expensive one. This rolling mechanism eats away at profits.
Below we show an example of a futures curve in contango, in this case, the corn curve as seen on 2019-06-12.
Let us now make the simplifying assumption that the front month price or spot market price of corn remains fixed at the current levels, here shown to be 430. If we have long exposure in corn and want to keep that long exposure, we need to sell the front month and buy the following contract. In the example above it implies you have to buy the C U9 Comdty contract for 438.25. This price will now decrease toward the spot market as it matures toward expiry, leaving you with a loss of -8.25 cents per bushel. Hence, if you want to profit from long exposure in a commodity with a curve that is in contago you need to clear the barrier set by rolling your position along the futures curve.Below we show an example of a curve in backwardation.
It is much easier to trade long exposure profitably in a commodity that is in backwardation. Similar to the case of corn we suppose the spot price for zinc is fixed at the current levels of 2617.5. When the front contract expires and we want to keep our long exposure, we have to sell the front month at 2617.5 and buy the next contract at 2559.5. Assuming the shape of the curve remaines constant this gives you a profit of 58 USD/MT.
The BCOM Index performed well from 2002 to just before the global financial crisis. During this period the energy complex was largely in backwardation. Since the energies play such a big part in the total performance of the index you would expect that the index will perform well in sustained periods of backwardation.
Another way to exploit the shape the the commodities future curves make use of calendar spreads. For more information on how this is done we refer the interested reader to
- Carry Bet Side and Size - Polar Star
- Bear Spread with Call - Polar Star
3.3 The effect of roll yield
One of the main reasons it is difficult to turn a profit by solely being long commodities is that you are constantly battling the contango. A great way to visualise the effect of contango is to calculate the roll adjusted continuous price curves of the commodities making up the index. The plots below show the roll adjusted prices in purple and the unajusted prices in green respectively. We follow the backwards adjusted convention where the far right, latest dates, have the same values for both the adjusted and normal prices. In the case of a commodity that predominantly trades in contango, NG is a good example, the historical prices will be shifted higher by the cummulative roll since the start of the time series. The inverse applies for a roll during a backwardation, here the contribution is a downward shift. In the plots below, when the purple curve is above the green curve for sustained periods of time it implies that the curve was in contango during the forward roll of the long exposure. We only show results for NG, C, CL, KC and KW.
For more on the effect of roll yield on inter commodity spreads see
- Deconstructing Futures Returns by Campbell and Company
- Sugar Spread and Curve Structure - Polar Star
- Roll vs Spread - Polar Star
- Relative Roll Proof of Principle Results - Polar Star
3.4 Index Proxy
The value of USD 1 invested at inception is represented in the equity curve below. For comparison we show the values for the backtest together with the original BCOM Index. Note that the backtest performs better than the original. The reason for this is twofold. Firstly, the commodities that were included in the calculation of the index has changed considerable over the years. A prime example is that of gasoline (XB), where the contract only started trading near the end of 2005. As mensioned earlier, we make use of the mean weights as determined from the average of the weights since 2015. If a commodity was not available for trade during an earlier time we normalise the resulting weight vector. This will result in a greater notional exposure in those commodities that were available. The start of the divergence between the two curves also seem to coinside with this timeframe. The general form of the two equity curves are still quite similar.
The tables below show the risk and return statistics of the backtested version of the BCOM Index. We consider various return and risk measures as well as a detailed drawdown report.
| Return Statistics | |
|---|---|
| Last Month | -0.77 |
| Year To Date | 3.40 |
| 3 Month ROR | -1.08 |
| 12 Month ROR | -5.58 |
| 36 Month ROR | -3.22 |
| Total Return | 41.15 |
| Compound ROR | 1.22 |
| Best Month | 12.64 |
| Win % | 53.80 |
| Risk Statistics | |
|---|---|
| Ann.Std.Deviation | 13.08 |
| Max. Drawdown | 57.29 |
| Month to Recover | 134.00 |
| Worst Month | -20.78 |
| Losing % | 46.20 |
| Avg Losing Month | -2.84 |
| Loss Deviation | 2.76 |
| Risk/Reward Statistics | |
|---|---|
| Sharpe Ratio | 0.09 |
| Sortino Ratio | 0.13 |
| Omega Ratio | 0.13 |
| Skewness | -0.53 |
| Kurtosis | 3.03 |
| Best | Worst | Average | Median | Last | Winning (%) | Avg. Pos. Period | Avg. Neg. Period | # Of Periods | |
|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 12.64 | -20.78 | 0.17 | 0.26 | -0.77 | 53.80 | 2.76 | -2.84 | 342 |
| 3 Month | 21.98 | -34.36 | 0.56 | 0.70 | -1.08 | 56.18 | 5.15 | -5.32 | 340 |
| 6 Month | 32.33 | -45.42 | 1.28 | 2.57 | -1.91 | 59.94 | 8.02 | -8.81 | 337 |
| 1 Year | 40.84 | -45.36 | 2.71 | 2.51 | -5.58 | 58.01 | 13.55 | -12.27 | 331 |
| 2 Year | 67.44 | -39.97 | 5.89 | 2.94 | -4.16 | 56.11 | 23.18 | -16.22 | 319 |
| 3 Year | 87.54 | -43.18 | 8.75 | 3.44 | -3.22 | 54.07 | 29.86 | -16.10 | 307 |
| 5 Year | 144.48 | -48.08 | 16.81 | 8.96 | -33.33 | 62.54 | 40.47 | -22.71 | 283 |
Drawdown Report:
| Depth (%) | Length (Months) | Recovery (Months) | Start | End |
|---|---|---|---|---|
| -57.29 | 134 | NA | 2008-07-31 | NA |
| -36.93 | 77 | 56 | 1997-06-30 | 2003-10-31 |
| -9.54 | 14 | 12 | 2006-08-31 | 2007-09-28 |
| -8.10 | 31 | 16 | 1991-11-29 | 1994-05-31 |
| -6.02 | 4 | 3 | 2008-03-31 | 2008-06-30 |
Time Window Analysis:
| 1 Month | 3 Month | 6 Month | 1 Year | 2 Year | 3 Year | 5 Year | |
|---|---|---|---|---|---|---|---|
| Best | 12.64 | 21.98 | 32.33 | 40.84 | 67.44 | 87.54 | 144.48 |
| Worst | -20.78 | -34.36 | -45.42 | -45.36 | -39.97 | -43.18 | -48.08 |
| Average | 0.17 | 0.56 | 1.28 | 2.71 | 5.89 | 8.75 | 16.81 |
| Median | 0.26 | 0.70 | 2.57 | 2.51 | 2.94 | 3.44 | 8.96 |
| Last | -0.77 | -1.08 | -1.91 | -5.58 | -4.16 | -3.22 | -33.33 |
| Winning (%) | 53.80 | 56.18 | 59.94 | 58.01 | 56.11 | 54.07 | 62.54 |
| Avg. Pos. Period | 2.76 | 5.15 | 8.02 | 13.55 | 23.18 | 29.86 | 40.47 |
| Avg. Neg. Period | -2.84 | -5.32 | -8.81 | -12.27 | -16.22 | -16.10 | -22.71 |
| # Of Periods | 342.00 | 340.00 | 337.00 | 331.00 | 319.00 | 307.00 | 283.00 |
3.5 Index Proxy Performance Attribution
In this section we break down the performance of the individual commodities and highlight periods of backwardation and contango. To this end, we define the spread
\[ S_{C,K} := P_{C,K} - P_{C,K'} \]
for each commodity \(C\) as the price difference between the front contract \(K\) and deferred contract, twelve months out from the front contract, \(K'\). If this number is negative the curve is in contango, if it is positive the curve is in backwardation.
In the plots below green and orange dots represent backwardation and contango periods respectively. Notice that, in general, the positive return contributions arrise during periods of backwardation. Conversely, the negative returns occur mostly during sustained periods of contango.
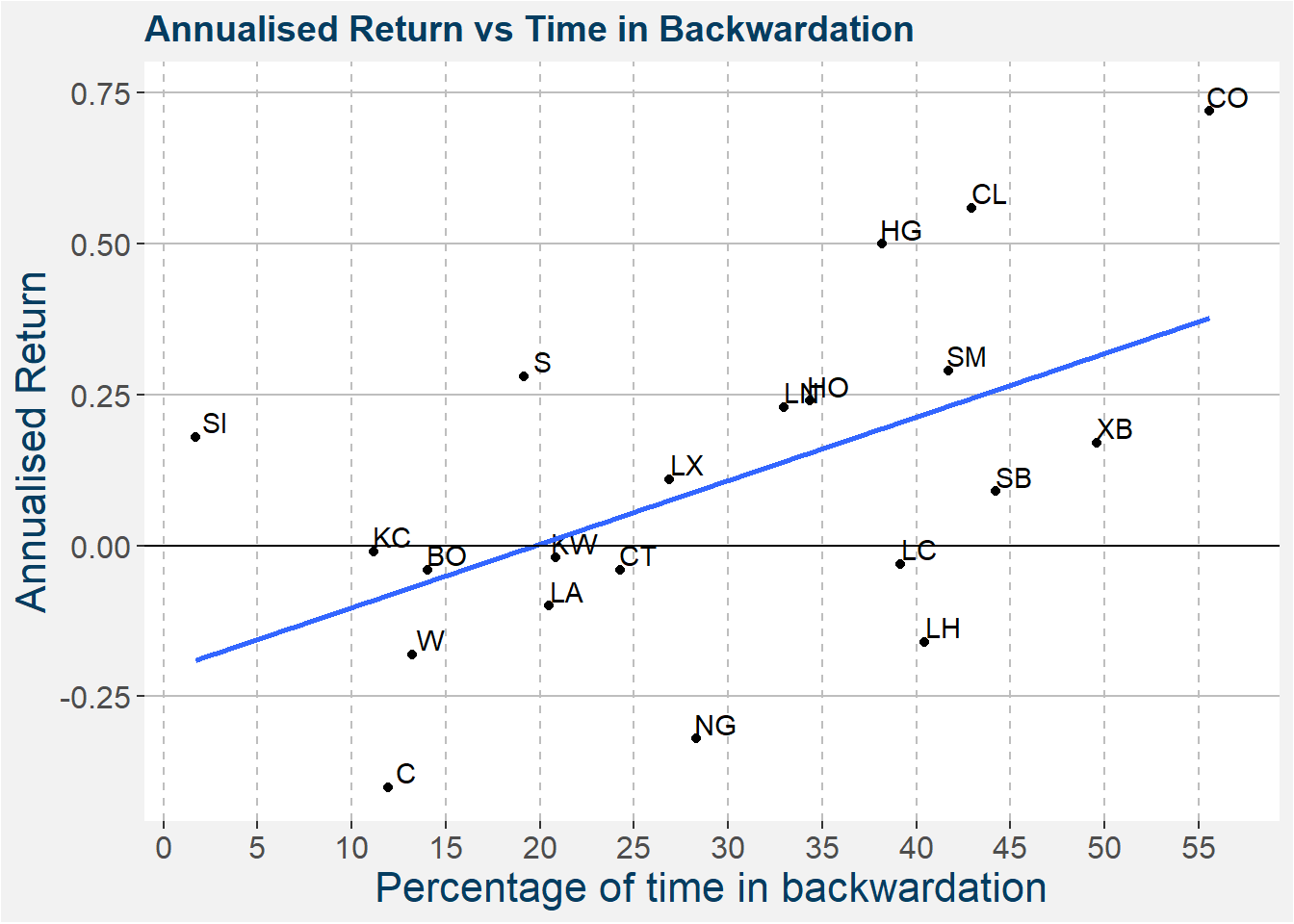
3.6 Curve Shape and Annualised Return
The image below shows the annualised return of each of the commodities in the long-only index proxy as a function of time spent in backwardation. The superimposed curve shows the best fit linear regression. From the image below is is clear that the more time a commodity spends in backwardation the greater it’s returns from a long-only point of view.
3.7 Long Backwardated Commodities
Here we modity the BCOM Index to only take long exposure in those commodities whose curves are in backwardation. The results below show the performance of the BCOM strategy after applying the backwardation filter. The results are shown on a logarithmic scale to make comparison over a long time period easier. Notice that performance of the two strategies are very similar up to the global financial crisis, however afterwards the backwardation filter model greatly outperforms the standard BCOM Index.
| Return Statistics | |
|---|---|
| Last Month | 0.07 |
| Year To Date | -3.61 |
| 3 Month ROR | -3.43 |
| 12 Month ROR | -5.86 |
| 36 Month ROR | -2.96 |
| Total Return | 223.44 |
| Compound ROR | 4.20 |
| Best Month | 13.93 |
| Win % | 51.75 |
| Risk Statistics | |
|---|---|
| Ann.Std.Deviation | 8.72 |
| Max. Drawdown | 20.20 |
| Month to Recover | 100.00 |
| Worst Month | -10.50 |
| Losing % | 47.08 |
| Avg Losing Month | -1.39 |
| Loss Deviation | 1.69 |
| Risk/Reward Statistics | |
|---|---|
| Sharpe Ratio | 0.48 |
| Sortino Ratio | 0.72 |
| Omega Ratio | 0.57 |
| Skewness | 0.51 |
| Kurtosis | 4.74 |
| Best | Worst | Average | Median | Last | Winning (%) | Avg. Pos. Period | Avg. Neg. Period | # Of Periods | |
|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 13.93 | -10.50 | 0.38 | 0.04 | 0.07 | 51.75 | 1.99 | -1.39 | 342 |
| 3 Month | 18.75 | -15.53 | 1.13 | 0.56 | -3.43 | 56.76 | 3.93 | -2.55 | 340 |
| 6 Month | 25.14 | -16.51 | 2.35 | 1.23 | -3.34 | 60.24 | 6.38 | -3.75 | 337 |
| 1 Year | 42.06 | -17.10 | 5.00 | 2.54 | -5.86 | 60.42 | 11.59 | -5.05 | 331 |
| 2 Year | 57.59 | -16.34 | 10.94 | 4.90 | -1.63 | 66.77 | 19.11 | -5.49 | 319 |
| 3 Year | 73.49 | -14.78 | 17.33 | 12.46 | -2.96 | 73.94 | 25.17 | -4.91 | 307 |
| 5 Year | 121.12 | -17.76 | 34.24 | 28.58 | -14.04 | 80.92 | 44.21 | -8.07 | 283 |
Drawdown Report:
| Depth (%) | Length (Months) | Recovery (Months) | Start | End |
|---|---|---|---|---|
| -20.20 | 100 | NA | 2011-05-31 | NA |
| -17.60 | 27 | 12 | 2000-12-29 | 2003-02-28 |
| -16.80 | 34 | 26 | 2008-07-31 | 2011-04-29 |
| -16.75 | 33 | 11 | 1997-06-30 | 2000-02-29 |
| -9.12 | 50 | 26 | 1991-11-29 | 1995-12-29 |
Time Window Analysis:
| 1 Month | 3 Month | 6 Month | 1 Year | 2 Year | 3 Year | 5 Year | |
|---|---|---|---|---|---|---|---|
| Best | 13.93 | 18.75 | 25.14 | 42.06 | 57.59 | 73.49 | 121.12 |
| Worst | -10.50 | -15.53 | -16.51 | -17.10 | -16.34 | -14.78 | -17.76 |
| Average | 0.38 | 1.13 | 2.35 | 5.00 | 10.94 | 17.33 | 34.24 |
| Median | 0.04 | 0.56 | 1.23 | 2.54 | 4.90 | 12.46 | 28.58 |
| Last | 0.07 | -3.43 | -3.34 | -5.86 | -1.63 | -2.96 | -14.04 |
| Winning (%) | 51.75 | 56.76 | 60.24 | 60.42 | 66.77 | 73.94 | 80.92 |
| Avg. Pos. Period | 1.99 | 3.93 | 6.38 | 11.59 | 19.11 | 25.17 | 44.21 |
| Avg. Neg. Period | -1.39 | -2.55 | -3.75 | -5.05 | -5.49 | -4.91 | -8.07 |
| # Of Periods | 342.00 | 340.00 | 337.00 | 331.00 | 319.00 | 307.00 | 283.00 |
3.8 Short Contango Commodities
Here we consider a short only portfolio with short exposure equal to the BCOM weights. Furthermore, we only take up short position in commodities in contango. It is interesting to note that the two equity curves are almost mirrors of each other.
| Return Statistics | |
|---|---|
| Last Month | -0.70 |
| Year To Date | -9.84 |
| 3 Month ROR | -4.80 |
| 12 Month ROR | -2.18 |
| 36 Month ROR | -3.85 |
| Total Return | 49.85 |
| Compound ROR | 1.43 |
| Best Month | 22.36 |
| Win % | 50.58 |
| Risk Statistics | |
|---|---|
| Ann.Std.Deviation | 12.38 |
| Max. Drawdown | 41.95 |
| Month to Recover | 85.00 |
| Worst Month | -12.25 |
| Losing % | 49.42 |
| Avg Losing Month | -2.31 |
| Loss Deviation | 2.19 |
| Risk/Reward Statistics | |
|---|---|
| Sharpe Ratio | 0.12 |
| Sortino Ratio | 0.19 |
| Omega Ratio | 0.16 |
| Skewness | 0.91 |
| Kurtosis | 5.54 |
| Best | Worst | Average | Median | Last | Winning (%) | Avg. Pos. Period | Avg. Neg. Period | # Of Periods | |
|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 22.36 | -12.25 | 0.18 | 0.03 | -0.70 | 50.58 | 2.61 | -2.31 | 342 |
| 3 Month | 44.63 | -17.07 | 0.58 | -0.15 | -4.80 | 48.82 | 5.19 | -3.81 | 340 |
| 6 Month | 62.51 | -18.41 | 1.29 | -0.72 | -4.56 | 45.40 | 9.21 | -5.30 | 337 |
| 1 Year | 72.54 | -22.06 | 2.64 | -0.81 | -2.18 | 45.62 | 14.37 | -7.20 | 331 |
| 2 Year | 63.91 | -31.63 | 5.00 | 0.06 | 1.08 | 50.16 | 19.64 | -9.73 | 319 |
| 3 Year | 67.30 | -32.03 | 7.67 | 2.16 | -3.85 | 55.05 | 22.99 | -11.10 | 307 |
| 5 Year | 76.54 | -31.85 | 13.22 | 9.64 | 34.03 | 62.54 | 29.97 | -14.74 | 283 |
Drawdown Report:
| Depth (%) | Length (Months) | Recovery (Months) | Start | End |
|---|---|---|---|---|
| -41.95 | 85 | 12 | 2002-02-28 | 2009-02-27 |
| -35.56 | 81 | 51 | 2009-03-31 | 2015-11-30 |
| -18.40 | 42 | NA | 2016-03-31 | NA |
| -17.64 | 30 | 19 | 1999-03-31 | 2001-08-31 |
| -14.77 | 79 | 49 | 1992-01-31 | 1998-07-31 |
Time Window Analysis:
| 1 Month | 3 Month | 6 Month | 1 Year | 2 Year | 3 Year | 5 Year | |
|---|---|---|---|---|---|---|---|
| Best | 22.36 | 44.63 | 62.51 | 72.54 | 63.91 | 67.30 | 76.54 |
| Worst | -12.25 | -17.07 | -18.41 | -22.06 | -31.63 | -32.03 | -31.85 |
| Average | 0.18 | 0.58 | 1.29 | 2.64 | 5.00 | 7.67 | 13.22 |
| Median | 0.03 | -0.15 | -0.72 | -0.81 | 0.06 | 2.16 | 9.64 |
| Last | -0.70 | -4.80 | -4.56 | -2.18 | 1.08 | -3.85 | 34.03 |
| Winning (%) | 50.58 | 48.82 | 45.40 | 45.62 | 50.16 | 55.05 | 62.54 |
| Avg. Pos. Period | 2.61 | 5.19 | 9.21 | 14.37 | 19.64 | 22.99 | 29.97 |
| Avg. Neg. Period | -2.31 | -3.81 | -5.30 | -7.20 | -9.73 | -11.10 | -14.74 |
| # Of Periods | 342.00 | 340.00 | 337.00 | 331.00 | 319.00 | 307.00 | 283.00 |
3.9 Combination Portfolio
Here we combine the two ideas where we only take long exposure in backwardated commodities while taking short exposure in contango commodities. We keep the BCOM Index weights. Below we compare the results to the BCOM proxy.
| Return Statistics | |
|---|---|
| Last Month | -1.58 |
| Year To Date | -14.27 |
| 3 Month ROR | -9.22 |
| 12 Month ROR | -8.76 |
| 36 Month ROR | -7.22 |
| Total Return | 436.09 |
| Compound ROR | 6.07 |
| Best Month | 22.36 |
| Win % | 56.43 |
| Risk Statistics | |
|---|---|
| Ann.Std.Deviation | 13.27 |
| Max. Drawdown | 27.72 |
| Month to Recover | 77.00 |
| Worst Month | -10.65 |
| Losing % | 43.57 |
| Avg Losing Month | -2.53 |
| Loss Deviation | 2.19 |
| Risk/Reward Statistics | |
|---|---|
| Sharpe Ratio | 0.46 |
| Sortino Ratio | 0.80 |
| Omega Ratio | 0.51 |
| Skewness | 0.77 |
| Kurtosis | 3.92 |
| Best | Worst | Average | Median | Last | Winning (%) | Avg. Pos. Period | Avg. Neg. Period | # Of Periods | |
|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 22.36 | -10.65 | 0.56 | 0.33 | -1.58 | 56.43 | 2.95 | -2.53 | 342 |
| 3 Month | 41.81 | -13.79 | 1.73 | 0.99 | -9.22 | 56.76 | 6.07 | -3.98 | 340 |
| 6 Month | 56.36 | -17.99 | 3.56 | 1.82 | -8.87 | 60.53 | 9.06 | -4.87 | 337 |
| 1 Year | 65.80 | -18.51 | 7.42 | 4.67 | -8.76 | 65.86 | 14.34 | -5.92 | 331 |
| 2 Year | 68.23 | -19.88 | 15.90 | 15.75 | -1.24 | 77.12 | 23.43 | -9.48 | 319 |
| 3 Year | 94.43 | -24.06 | 26.06 | 24.46 | -7.22 | 82.41 | 33.73 | -9.85 | 307 |
| 5 Year | 144.49 | -19.80 | 50.39 | 43.23 | 16.02 | 93.99 | 54.20 | -9.16 | 283 |
Drawdown Report:
| Depth (%) | Length (Months) | Recovery (Months) | Start | End |
|---|---|---|---|---|
| -27.72 | 77 | 32 | 2009-03-31 | 2015-07-31 |
| -20.50 | 44 | NA | 2016-01-29 | NA |
| -20.31 | 56 | 25 | 1991-11-29 | 1996-06-28 |
| -14.98 | 24 | 13 | 2002-01-31 | 2003-12-31 |
| -11.56 | 14 | 12 | 2006-10-31 | 2007-11-30 |
Time Window Analysis:
| 1 Month | 3 Month | 6 Month | 1 Year | 2 Year | 3 Year | 5 Year | |
|---|---|---|---|---|---|---|---|
| Best | 22.36 | 41.81 | 56.36 | 65.80 | 68.23 | 94.43 | 144.49 |
| Worst | -10.65 | -13.79 | -17.99 | -18.51 | -19.88 | -24.06 | -19.80 |
| Average | 0.56 | 1.73 | 3.56 | 7.42 | 15.90 | 26.06 | 50.39 |
| Median | 0.33 | 0.99 | 1.82 | 4.67 | 15.75 | 24.46 | 43.23 |
| Last | -1.58 | -9.22 | -8.87 | -8.76 | -1.24 | -7.22 | 16.02 |
| Winning (%) | 56.43 | 56.76 | 60.53 | 65.86 | 77.12 | 82.41 | 93.99 |
| Avg. Pos. Period | 2.95 | 6.07 | 9.06 | 14.34 | 23.43 | 33.73 | 54.20 |
| Avg. Neg. Period | -2.53 | -3.98 | -4.87 | -5.92 | -9.48 | -9.85 | -9.16 |
| # Of Periods | 342.00 | 340.00 | 337.00 | 331.00 | 319.00 | 307.00 | 283.00 |
4 Trend System
In this section we explore the use of a trend system on two different universes of commodities. Here a trend system adds value because it has a built in risk management system that allows winners to run while stopping out losing trades. In the first case we only consider the BCOM commodities. Secondly we show the added benefit of including commodities outside of the BCOM Index.
4.1 BCOM commodities
Because of the nature of the curve structure present in commodities we can trade a diversified portfolio of commodities in a profitable way using a trend system. Below we use only the commodities contained in the BCOM index in the Polar Star Trend Strategy. For more information the interested reader is referred to this post on designing a trend following strategy.
Below we present the equity curves of the backtested BCOM and Polar Star trend following model.
| Return Statistics | |
|---|---|
| Last Month | 0.66 |
| Year To Date | -0.78 |
| 3 Month ROR | 0.82 |
| 12 Month ROR | 13.73 |
| 36 Month ROR | -24.21 |
| Total Return | 3003.21 |
| Compound ROR | 12.85 |
| Best Month | 32.35 |
| Win % | 53.96 |
| Risk Statistics | |
|---|---|
| Ann.Std.Deviation | 23.44 |
| Max. Drawdown | 42.13 |
| Month to Recover | 41.00 |
| Worst Month | -12.85 |
| Losing % | 46.04 |
| Avg Losing Month | -4.17 |
| Loss Deviation | 3.02 |
| Risk/Reward Statistics | |
|---|---|
| Sharpe Ratio | 0.55 |
| Sortino Ratio | 1.23 |
| Omega Ratio | 0.64 |
| Skewness | 0.98 |
| Kurtosis | 2.75 |
| Best | Worst | Average | Median | Last | Winning (%) | Avg. Pos. Period | Avg. Neg. Period | # Of Periods | |
|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 32.35 | -12.85 | 1.23 | 0.49 | 0.66 | 53.96 | 5.84 | -4.17 | 341 |
| 3 Month | 65.19 | -18.22 | 3.69 | 2.58 | 0.82 | 59.59 | 10.65 | -6.58 | 339 |
| 6 Month | 78.93 | -23.14 | 7.58 | 5.02 | -0.78 | 61.90 | 17.17 | -8.01 | 336 |
| 1 Year | 104.30 | -25.26 | 15.62 | 11.92 | 13.73 | 70.00 | 26.75 | -10.35 | 330 |
| 2 Year | 151.85 | -39.65 | 33.31 | 29.69 | -9.90 | 81.76 | 44.23 | -15.64 | 318 |
| 3 Year | 249.49 | -35.82 | 55.17 | 49.70 | -24.21 | 85.29 | 67.45 | -16.02 | 306 |
| 5 Year | 287.80 | -5.86 | 109.09 | 79.58 | 7.84 | 97.87 | 111.55 | -4.18 | 282 |
Drawdown Report:
| Depth (%) | Length (Months) | Recovery (Months) | Start | End |
|---|---|---|---|---|
| -42.13 | 41 | NA | 2016-03-31 | NA |
| -28.57 | 29 | 7 | 2001-11-30 | 2004-03-31 |
| -25.79 | 22 | 5 | 2009-03-31 | 2010-12-31 |
| -25.67 | 41 | 20 | 2011-05-31 | 2014-09-30 |
| -25.02 | 22 | 6 | 2004-04-30 | 2006-01-31 |
Time Window Analysis:
| 1 Month | 3 Month | 6 Month | 1 Year | 2 Year | 3 Year | 5 Year | |
|---|---|---|---|---|---|---|---|
| Best | 32.35 | 65.19 | 78.93 | 104.30 | 151.85 | 249.49 | 287.80 |
| Worst | -12.85 | -18.22 | -23.14 | -25.26 | -39.65 | -35.82 | -5.86 |
| Average | 1.23 | 3.69 | 7.58 | 15.62 | 33.31 | 55.17 | 109.09 |
| Median | 0.49 | 2.58 | 5.02 | 11.92 | 29.69 | 49.70 | 79.58 |
| Last | 0.66 | 0.82 | -0.78 | 13.73 | -9.90 | -24.21 | 7.84 |
| Winning (%) | 53.96 | 59.59 | 61.90 | 70.00 | 81.76 | 85.29 | 97.87 |
| Avg. Pos. Period | 5.84 | 10.65 | 17.17 | 26.75 | 44.23 | 67.45 | 111.55 |
| Avg. Neg. Period | -4.17 | -6.58 | -8.01 | -10.35 | -15.64 | -16.02 | -4.18 |
| # Of Periods | 341.00 | 339.00 | 336.00 | 330.00 | 318.00 | 306.00 | 282.00 |
4.2 Larger universe of commodities
Here we extend the trend system to take into account a greater number of commodities as well as two parts of the futures curve. The effect of this further diversification is substantial.
Below we present the equity curves of the backtested BCOM and Polar Star trend following model.
| Return Statistics | |
|---|---|
| Last Month | 0.59 |
| Year To Date | 3.16 |
| 3 Month ROR | 5.23 |
| 12 Month ROR | 19.71 |
| 36 Month ROR | 1.18 |
| Total Return | 10227.97 |
| Compound ROR | 17.73 |
| Best Month | 44.08 |
| Win % | 56.89 |
| Risk Statistics | |
|---|---|
| Ann.Std.Deviation | 21.68 |
| Max. Drawdown | 41.79 |
| Month to Recover | 47.00 |
| Worst Month | -11.32 |
| Losing % | 43.11 |
| Avg Losing Month | -3.48 |
| Loss Deviation | 2.62 |
| Risk/Reward Statistics | |
|---|---|
| Sharpe Ratio | 0.82 |
| Sortino Ratio | 1.95 |
| Omega Ratio | 1.03 |
| Skewness | 1.53 |
| Kurtosis | 7.20 |
| Best | Worst | Average | Median | Last | Winning (%) | Avg. Pos. Period | Avg. Neg. Period | # Of Periods | |
|---|---|---|---|---|---|---|---|---|---|
| 1 Month | 44.08 | -11.32 | 1.55 | 1.08 | 0.59 | 56.89 | 5.37 | -3.48 | 341 |
| 3 Month | 84.24 | -15.25 | 4.79 | 3.58 | 5.23 | 64.31 | 10.59 | -5.68 | 339 |
| 6 Month | 116.12 | -26.58 | 9.96 | 7.85 | 3.16 | 69.05 | 17.90 | -7.78 | 336 |
| 1 Year | 165.97 | -28.72 | 21.13 | 17.71 | 19.71 | 74.24 | 31.87 | -9.83 | 330 |
| 2 Year | 272.37 | -35.94 | 46.60 | 39.30 | 10.30 | 84.28 | 58.18 | -15.49 | 318 |
| 3 Year | 367.65 | -37.96 | 77.05 | 64.06 | 1.18 | 87.91 | 90.04 | -17.39 | 306 |
| 5 Year | 469.46 | -19.35 | 155.78 | 147.07 | 44.71 | 97.16 | 160.69 | -12.35 | 282 |
Drawdown Report:
| Depth (%) | Length (Months) | Recovery (Months) | Start | End |
|---|---|---|---|---|
| -41.79 | 47 | 14 | 2011-03-31 | 2015-01-30 |
| -28.64 | 46 | NA | 2015-10-30 | NA |
| -26.48 | 18 | 6 | 2004-08-31 | 2006-01-31 |
| -19.32 | 20 | 2 | 2009-03-31 | 2010-10-29 |
| -15.87 | 7 | 3 | 1993-06-30 | 1993-12-31 |
Time Window Analysis:
| 1 Month | 3 Month | 6 Month | 1 Year | 2 Year | 3 Year | 5 Year | |
|---|---|---|---|---|---|---|---|
| Best | 44.08 | 84.24 | 116.12 | 165.97 | 272.37 | 367.65 | 469.46 |
| Worst | -11.32 | -15.25 | -26.58 | -28.72 | -35.94 | -37.96 | -19.35 |
| Average | 1.55 | 4.79 | 9.96 | 21.13 | 46.60 | 77.05 | 155.78 |
| Median | 1.08 | 3.58 | 7.85 | 17.71 | 39.30 | 64.06 | 147.07 |
| Last | 0.59 | 5.23 | 3.16 | 19.71 | 10.30 | 1.18 | 44.71 |
| Winning (%) | 56.89 | 64.31 | 69.05 | 74.24 | 84.28 | 87.91 | 97.16 |
| Avg. Pos. Period | 5.37 | 10.59 | 17.90 | 31.87 | 58.18 | 90.04 | 160.69 |
| Avg. Neg. Period | -3.48 | -5.68 | -7.78 | -9.83 | -15.49 | -17.39 | -12.35 |
| # Of Periods | 341.00 | 339.00 | 336.00 | 330.00 | 318.00 | 306.00 | 282.00 |
5 Conclusions
- The curve shape dominates the returns from long-only commodity portfolios
- In general, the long-only commodity approach only works in backwardated markets
- Better risk adjusted returns can be achieved by:
- adding short poisitions,
- extending the universe of commodities, and
- adding risk management:
- similar to trendfollowing
- letting winners run
- spotting losers out