Coffee Arbitrage Feature Importance

Last updated on 12 min read Feature Importance, Coffee

Introduction

In this post we explore the feature importance of the Arabica vs Robusta coffee arbitrage. As input features we use Arabica and Robusta consumer stocks broken down by

  • GCA - Green Coffee Association
  • EU - European Union
  • Japan
  • Total
  • Importing Consumptin
  • Importing S/C - Total/Importing Consumption

To add a measure of possible seasonality we also include the number of days until expiry of the first contract in the arbitrage.

We model both the spread and ratio separately as they can have quite different behaviour. The feature importance is done with classifiction models were we bin the prices into deciles. The model is then trained to find the price decile. We use six techniques to compare feature importance of the trained classification:

  • MDI - Mean Decrease Impurity
  • MDA - Mean Decrease Accuracy
  • SFI - Single Feature Importance
  • CFI - Clustered Feature Importance
  • SHAP - Shapley Feature Importance
  • PCA - Principle component analysis

The PCA method is used to calculate the weighted tau statistic. The idea is to see how correlated the principle components and the chosen features are. The higher the weighted tau number the better.

Next we train regression modeld on the reduced feature space. These models are thes used within the fingerprint method of Li, Turkington and Yazdani to study the linear and non-linear effects present in the resulting models. This method helps us eleminate even more redundant features by allowing us to ony keep those features responsible for the majority of the linear, non-linear and interaction affects present within the features.

Finally, after the main features have been extracted we train regression models on the chosen features and make these results available in Shiny.

F

F - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
F MDA 0.692 ratio
F CFI 0.171 ratio
F SHAP 0.036 ratio
F SFI -0.016 ratio
F MDI -0.507 ratio
code method weighted_tau type
F SFI 0.545 spread
F MDA 0.352 spread
F SHAP 0.070 spread
F MDI -0.042 spread

Below we show the feature importances of the top positive weighted tau methods.

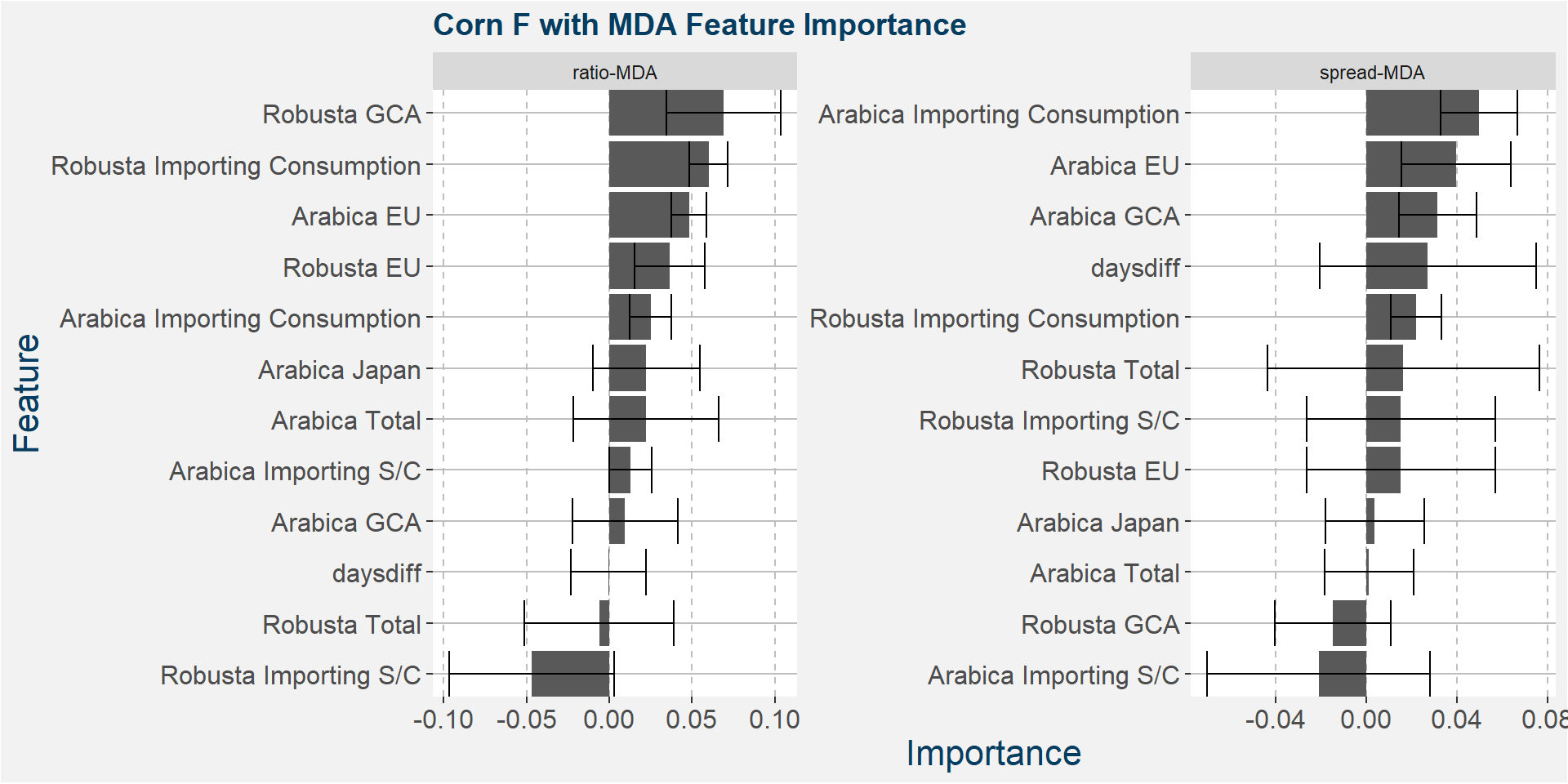
F - Fingerprint Method

The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

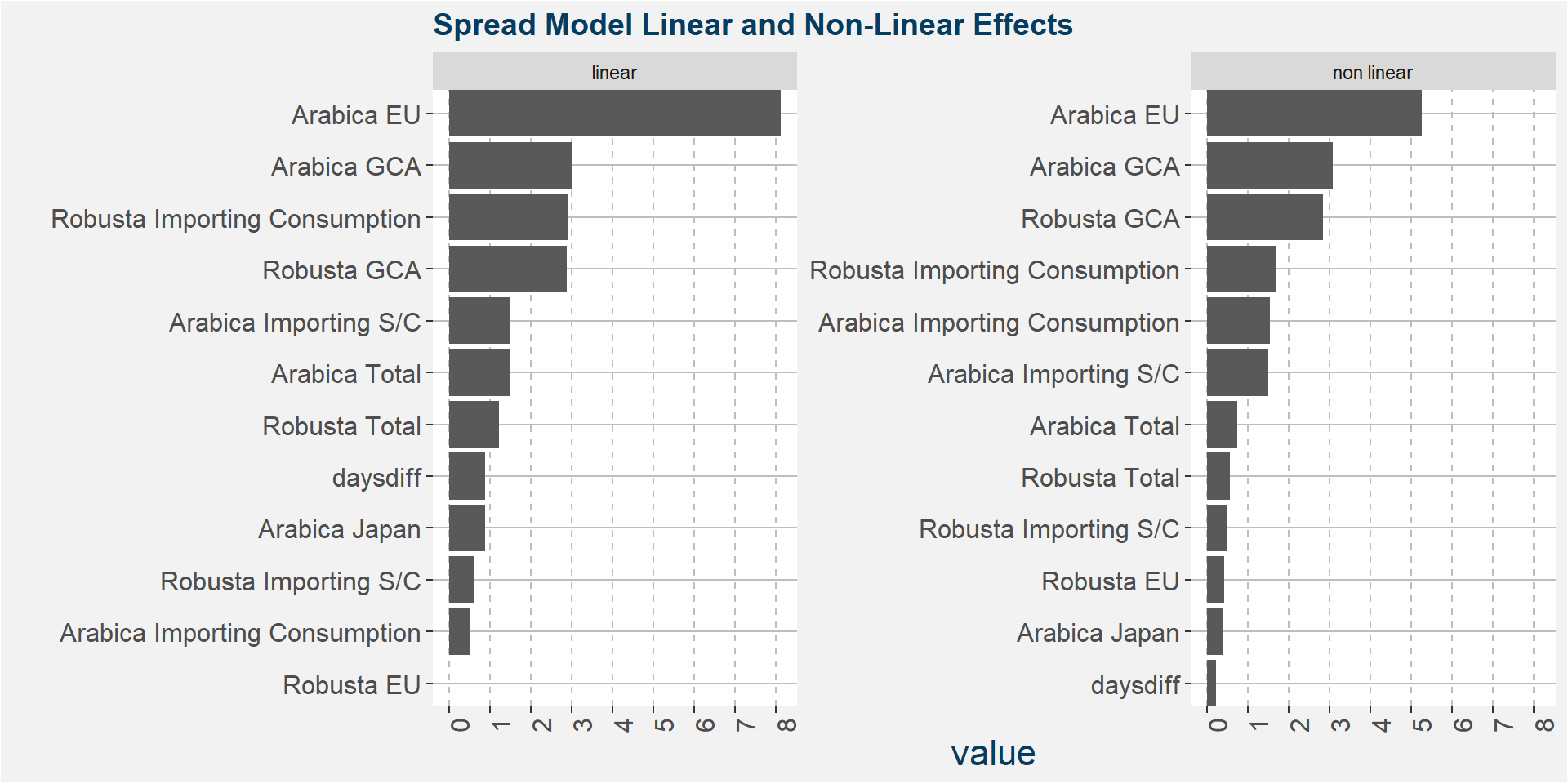
The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

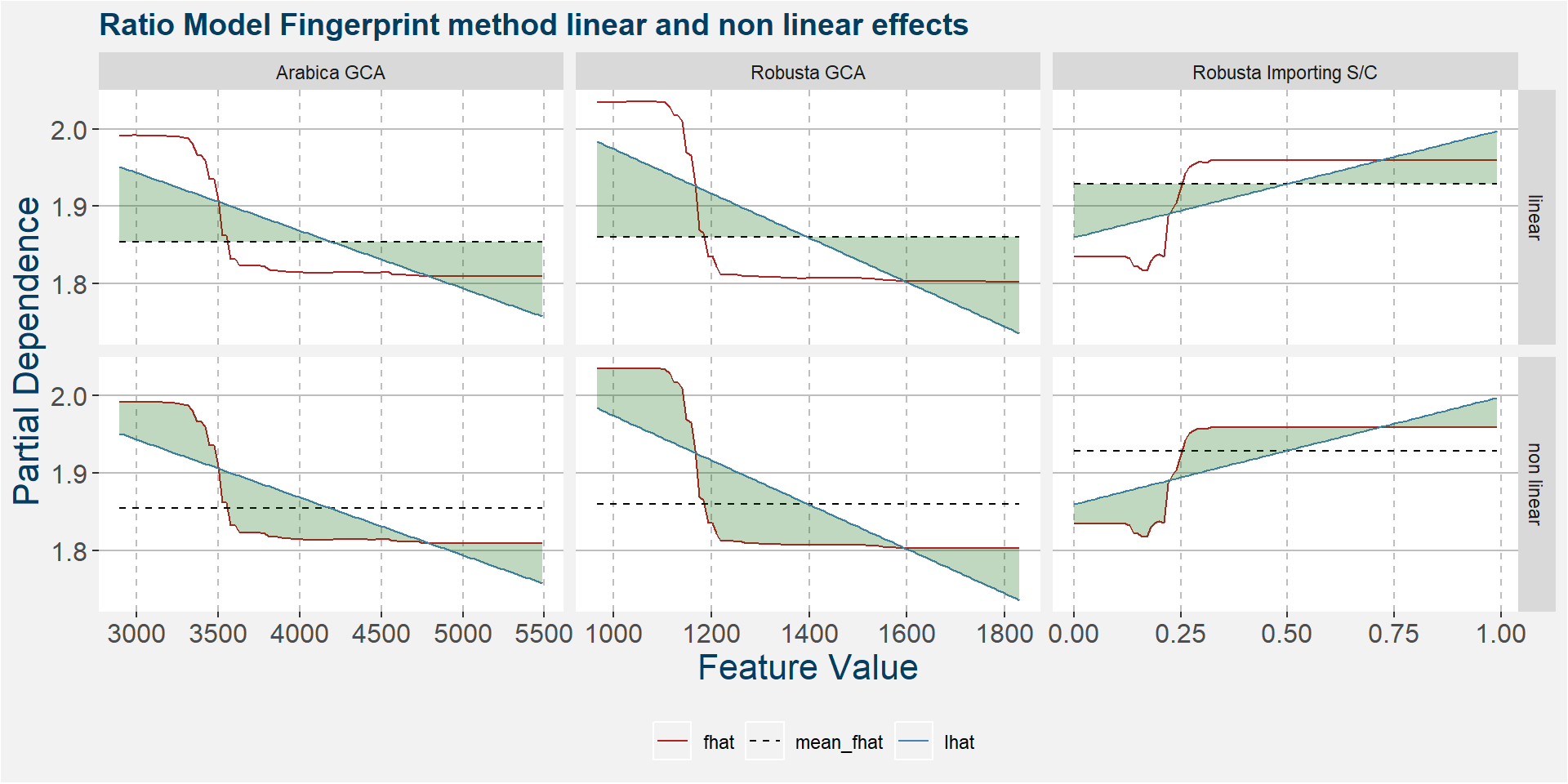
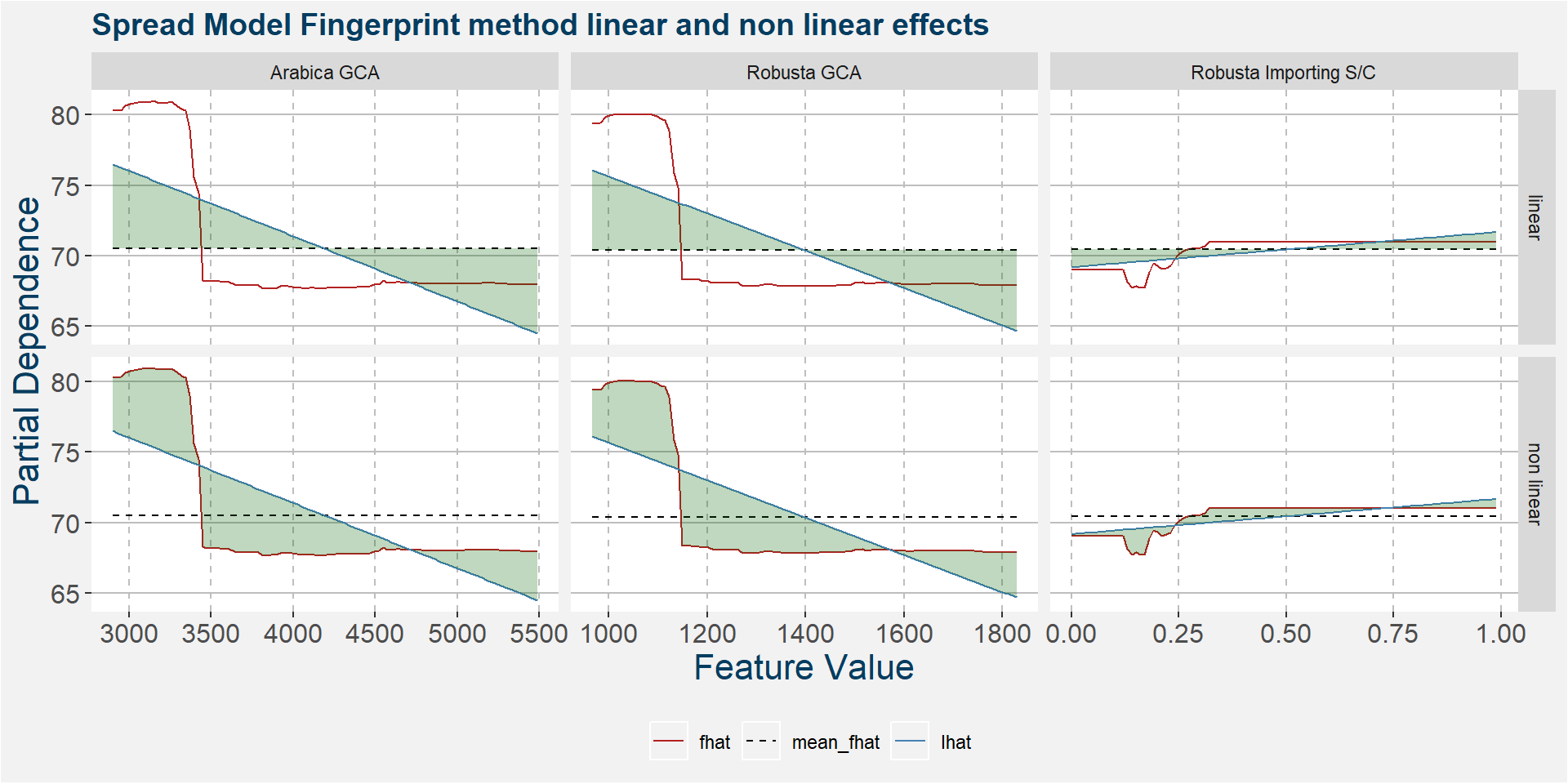
F - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.57 0.59 0.74
ratio oob NA NA 0.68
ratio out of sample 0.52 0.55 0.61
spread in sample 0.53 0.53 0.84
spread oob NA NA 0.63
spread out of sample 0.50 0.50 0.70

H

H - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
H MDA 0.519 ratio
H SHAP 0.401 ratio
H SFI 0.383 ratio
H CFI 0.368 ratio
H MDI -0.228 ratio
code method weighted_tau type
H SFI 0.296 spread
H SHAP 0.281 spread
H MDA -0.233 spread
H MDI -0.267 spread

Below we show the feature importances of the top positive weighted tau methods.

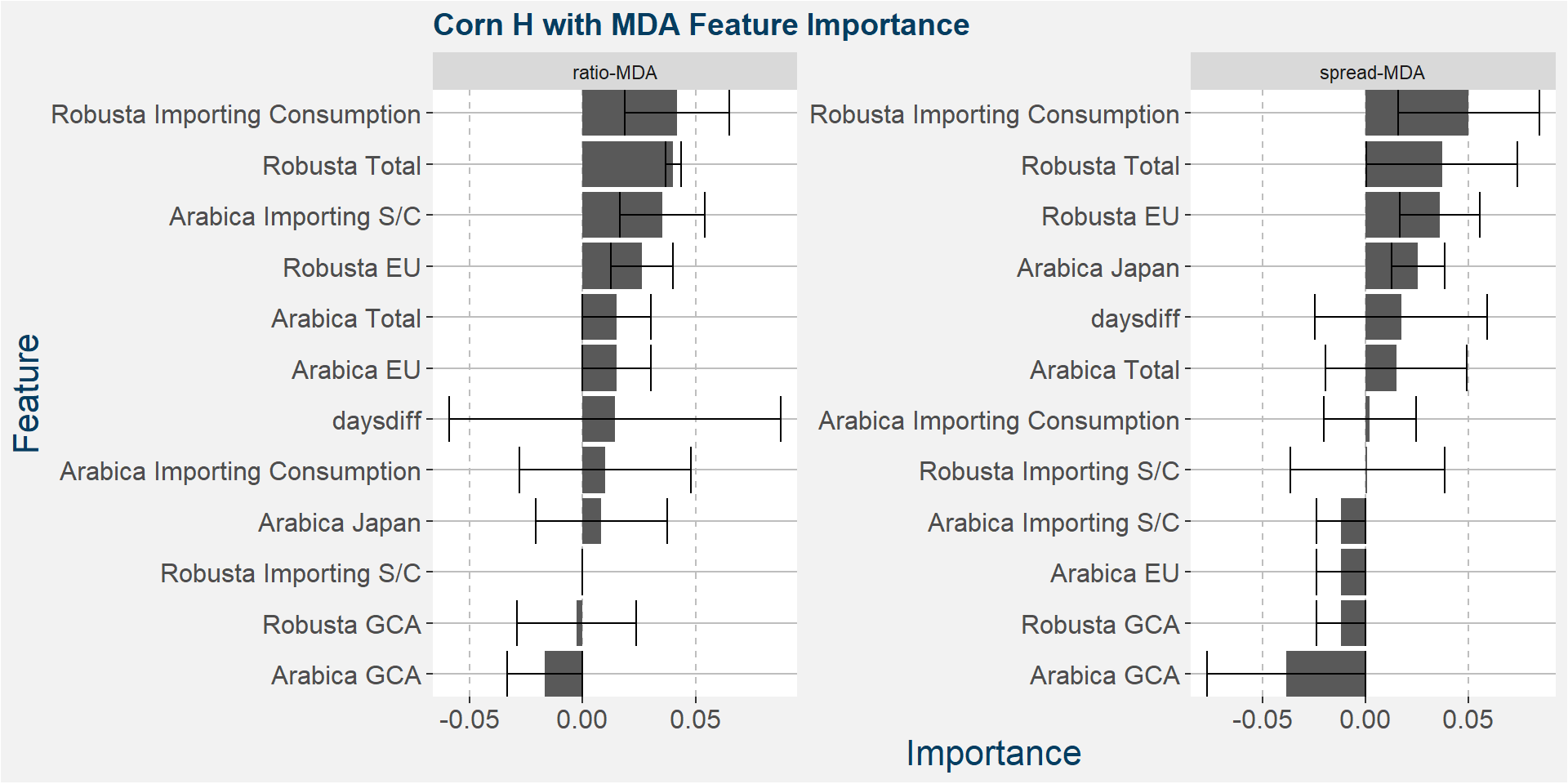
H - Fingerprint Method

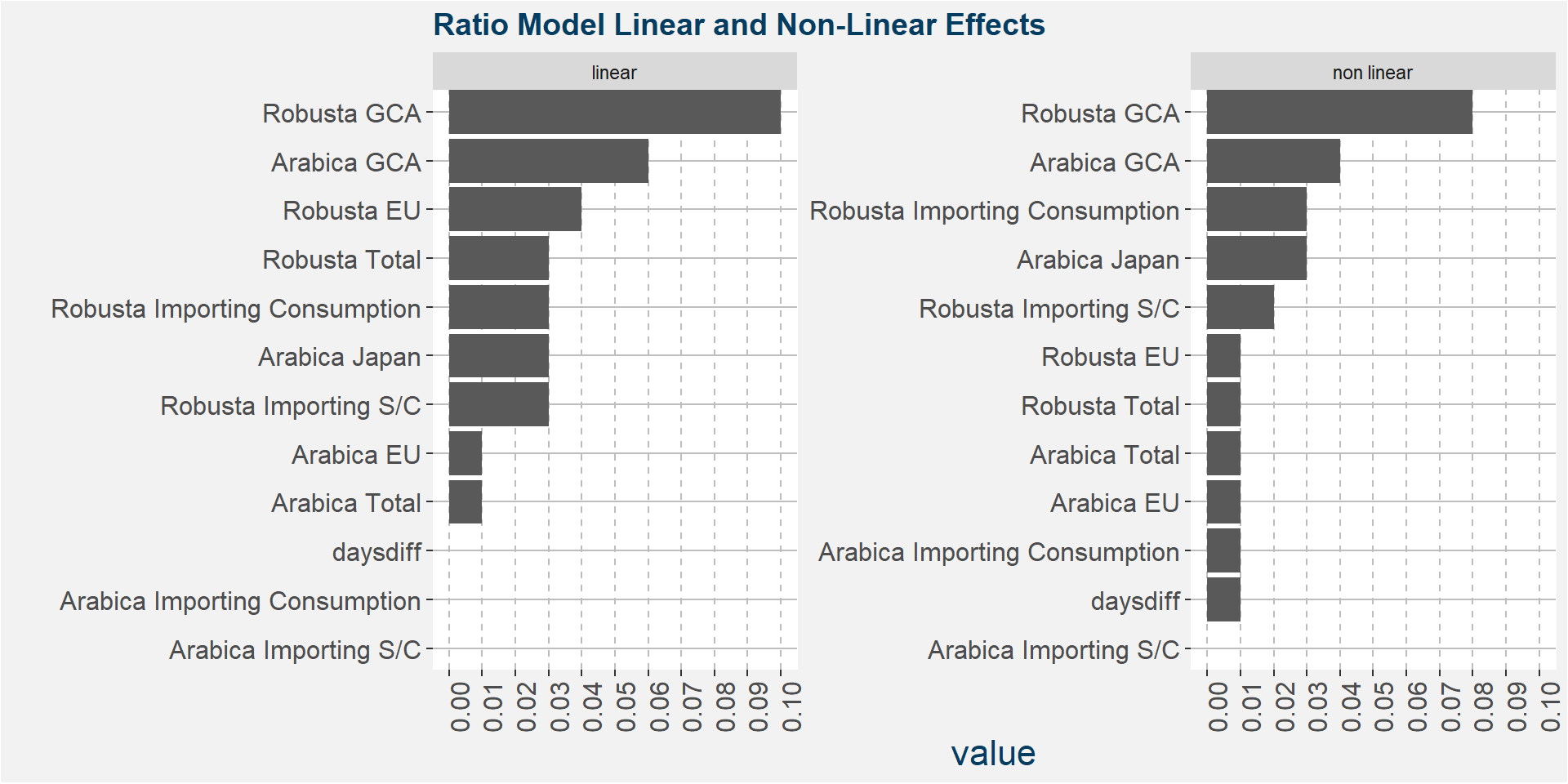
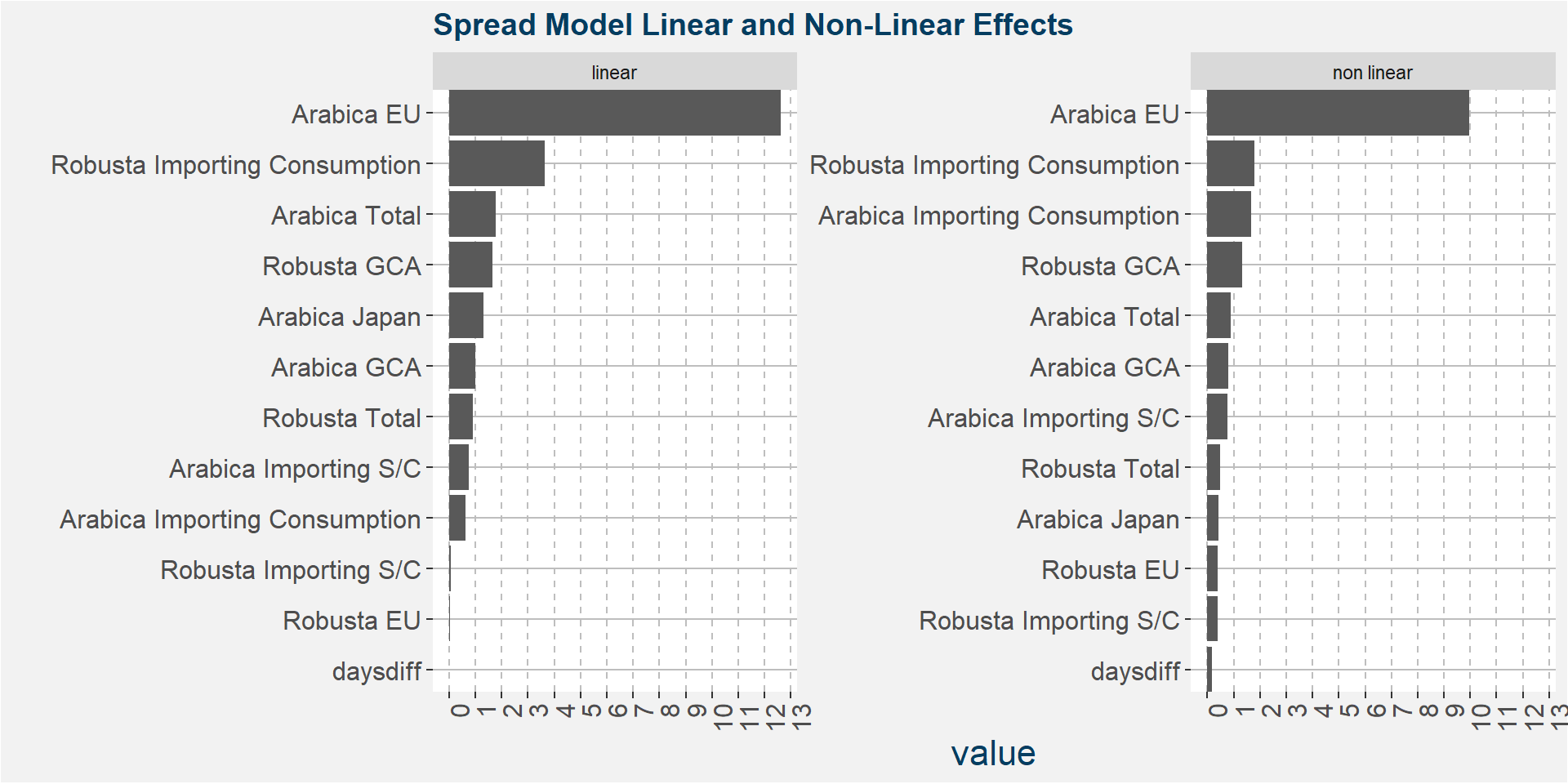
The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

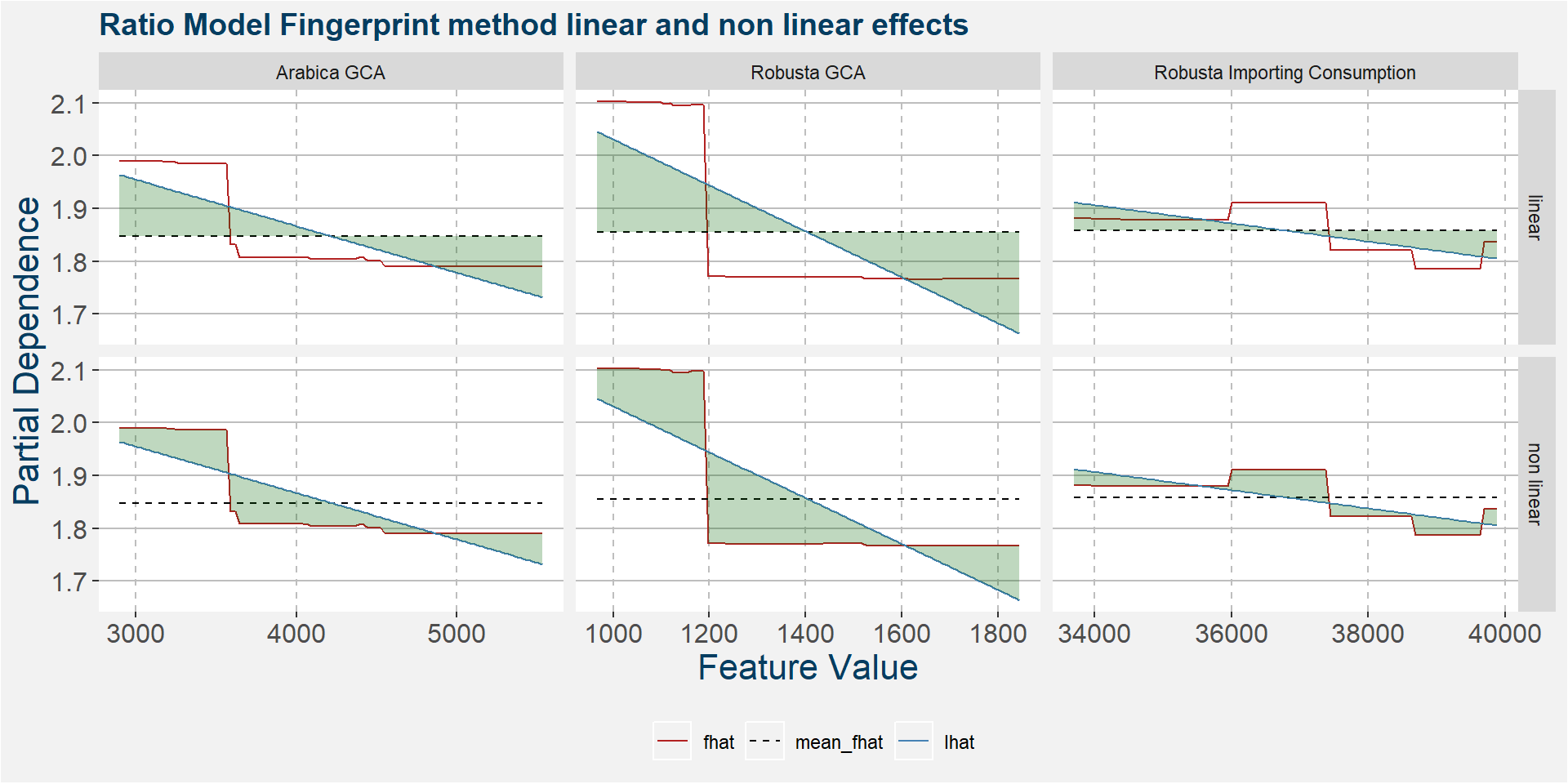
The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

H - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.55 0.65 0.78
ratio oob NA NA -0.15
ratio out of sample 0.55 0.65 0.66
spread in sample 0.54 0.55 0.91
spread oob NA NA 0.47
spread out of sample 0.46 0.46 0.79

K

K - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
K CFI 0.171 ratio
K SFI 0.147 ratio
K MDA 0.018 ratio
K SHAP -0.121 ratio
K MDI -0.522 ratio
code method weighted_tau type
K SFI 0.350 spread
K SHAP 0.181 spread
K MDI 0.013 spread
K MDA -0.188 spread

Below we show the feature importances of the top positive weighted tau methods.

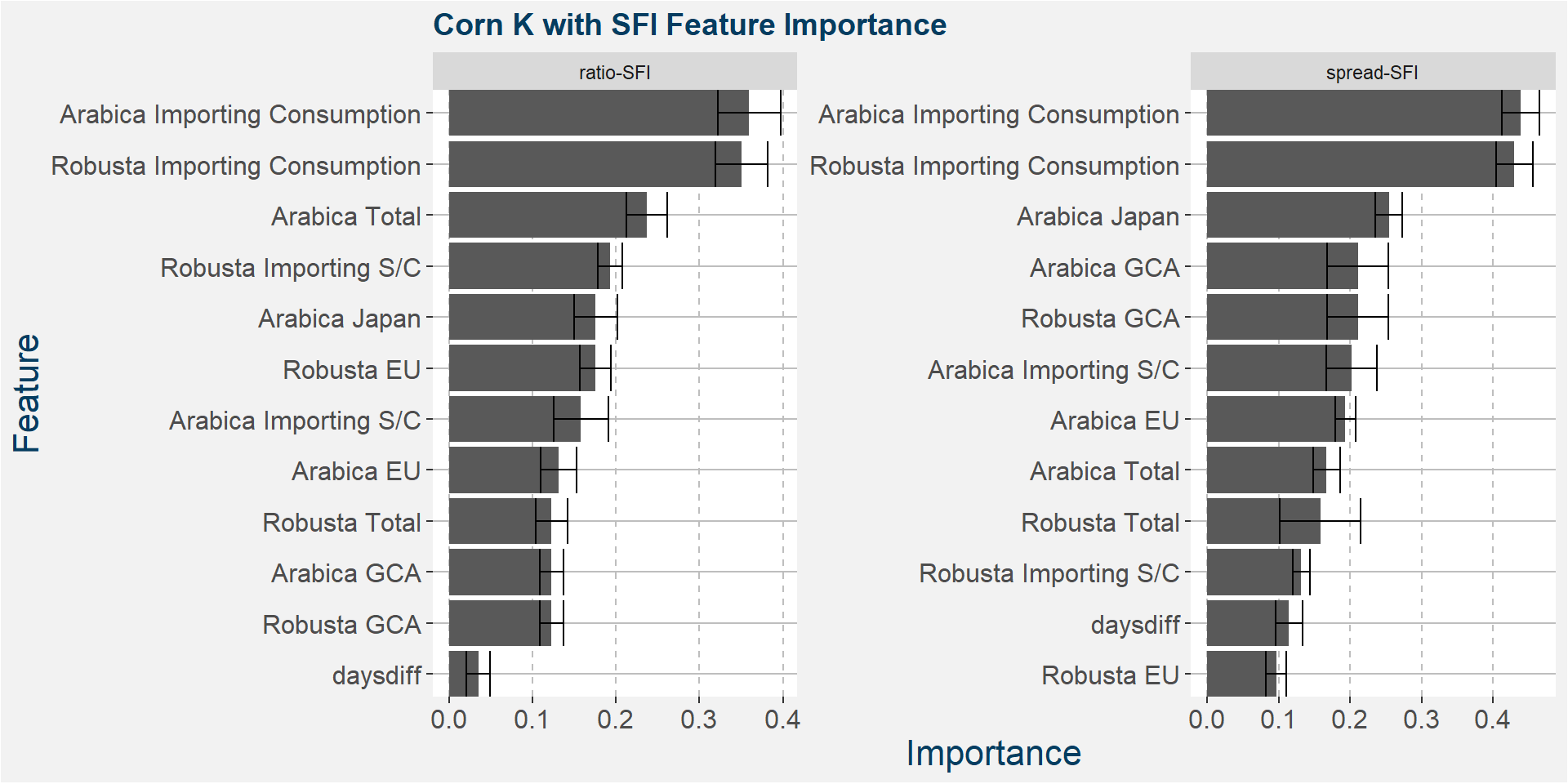
K - Fingerprint Method

The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

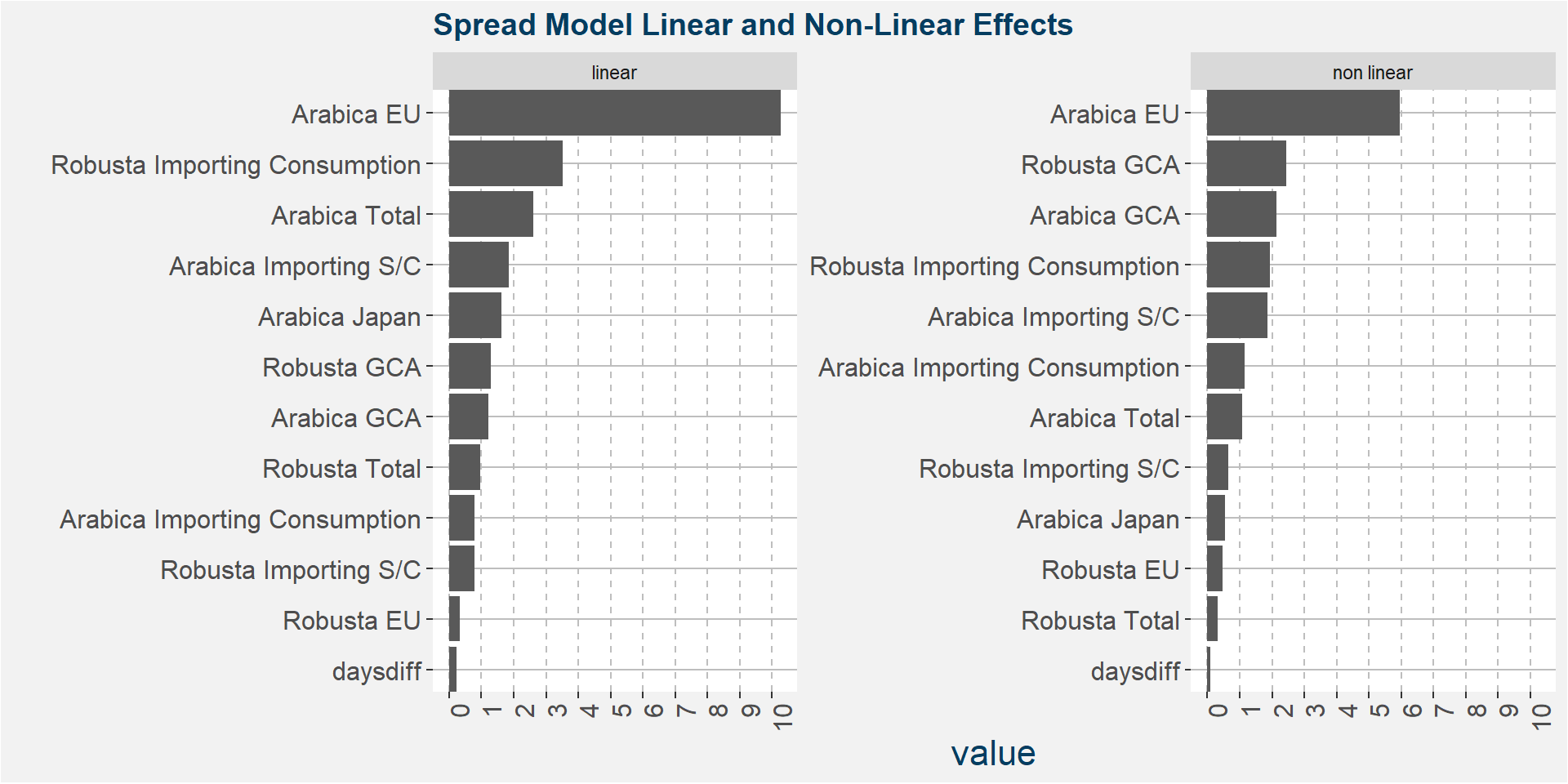
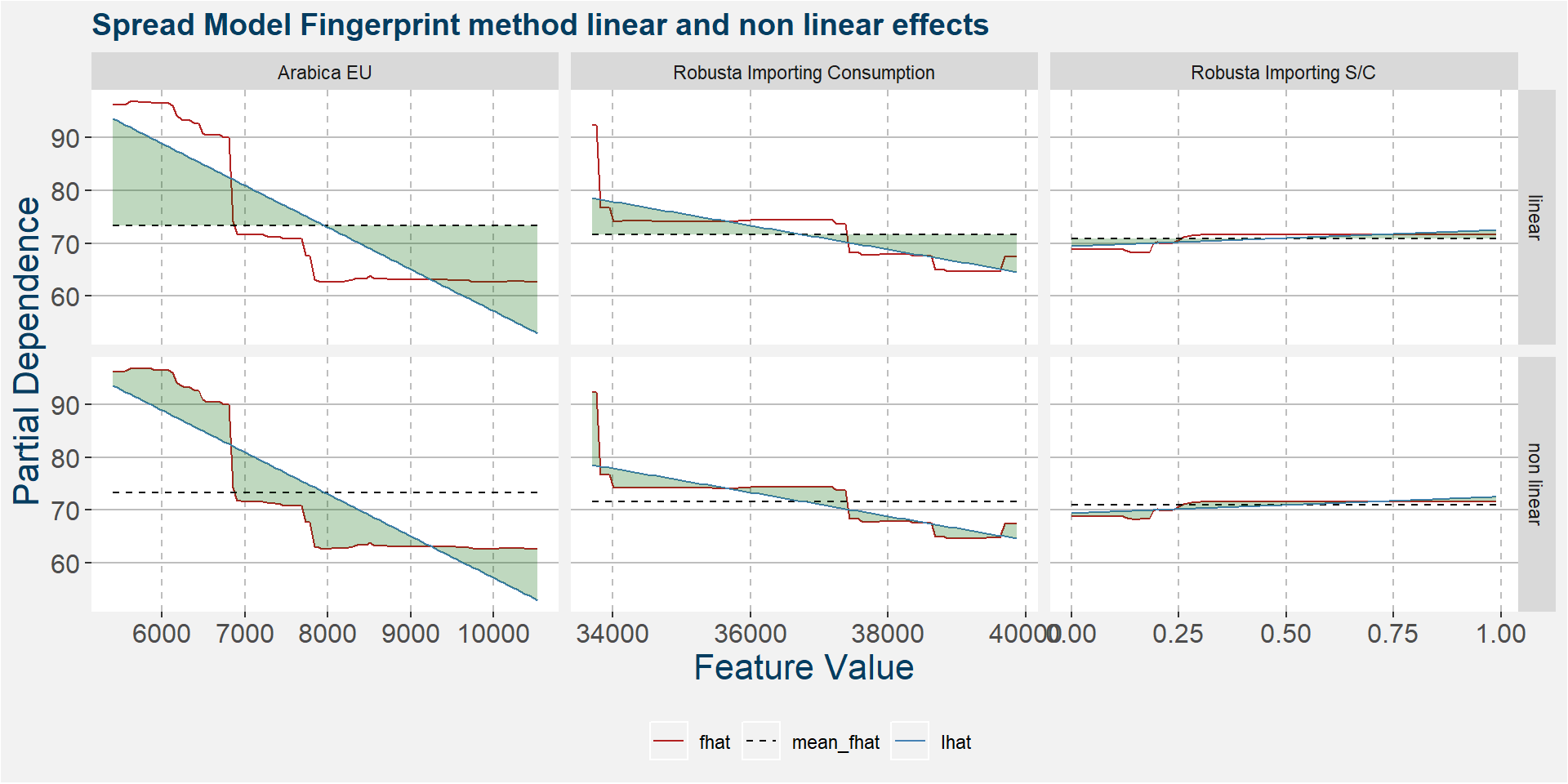
The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

K - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.59 0.62 0.92
ratio oob NA NA 0.73
ratio out of sample 0.50 0.52 0.63
spread in sample 0.54 0.54 0.95
spread oob NA NA 0.78
spread out of sample 0.41 0.41 0.78

N

N - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
N CFI 0.336 ratio
N MDA 0.242 ratio
N SFI 0.118 ratio
N MDI 0.117 ratio
N SHAP 0.032 ratio
code method weighted_tau type
N SFI 0.198 spread
N SHAP 0.142 spread
N MDI -0.119 spread
N MDA -0.156 spread

Below we show the feature importances of the top positive weighted tau methods.

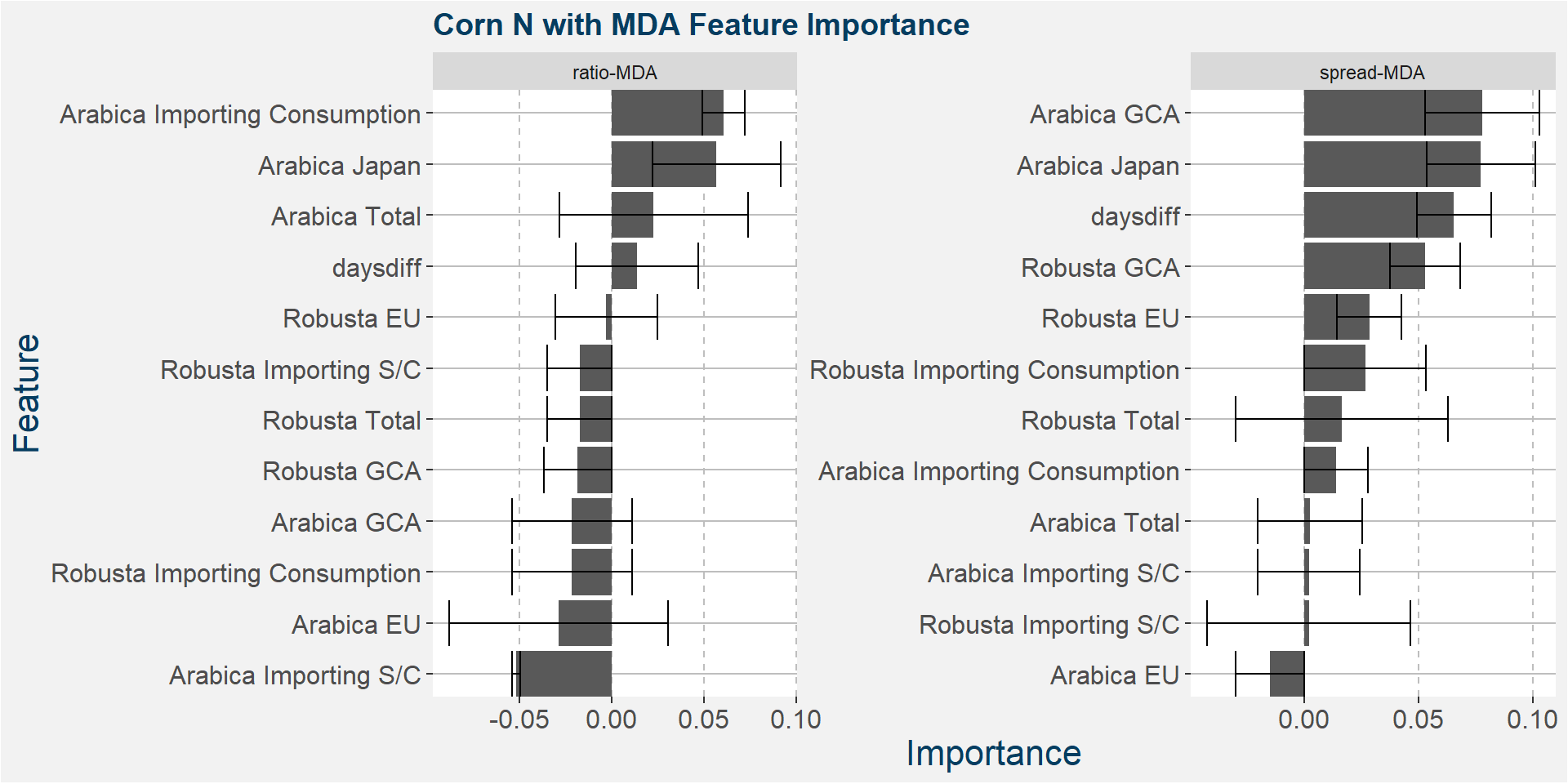
N - Fingerprint Method

The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

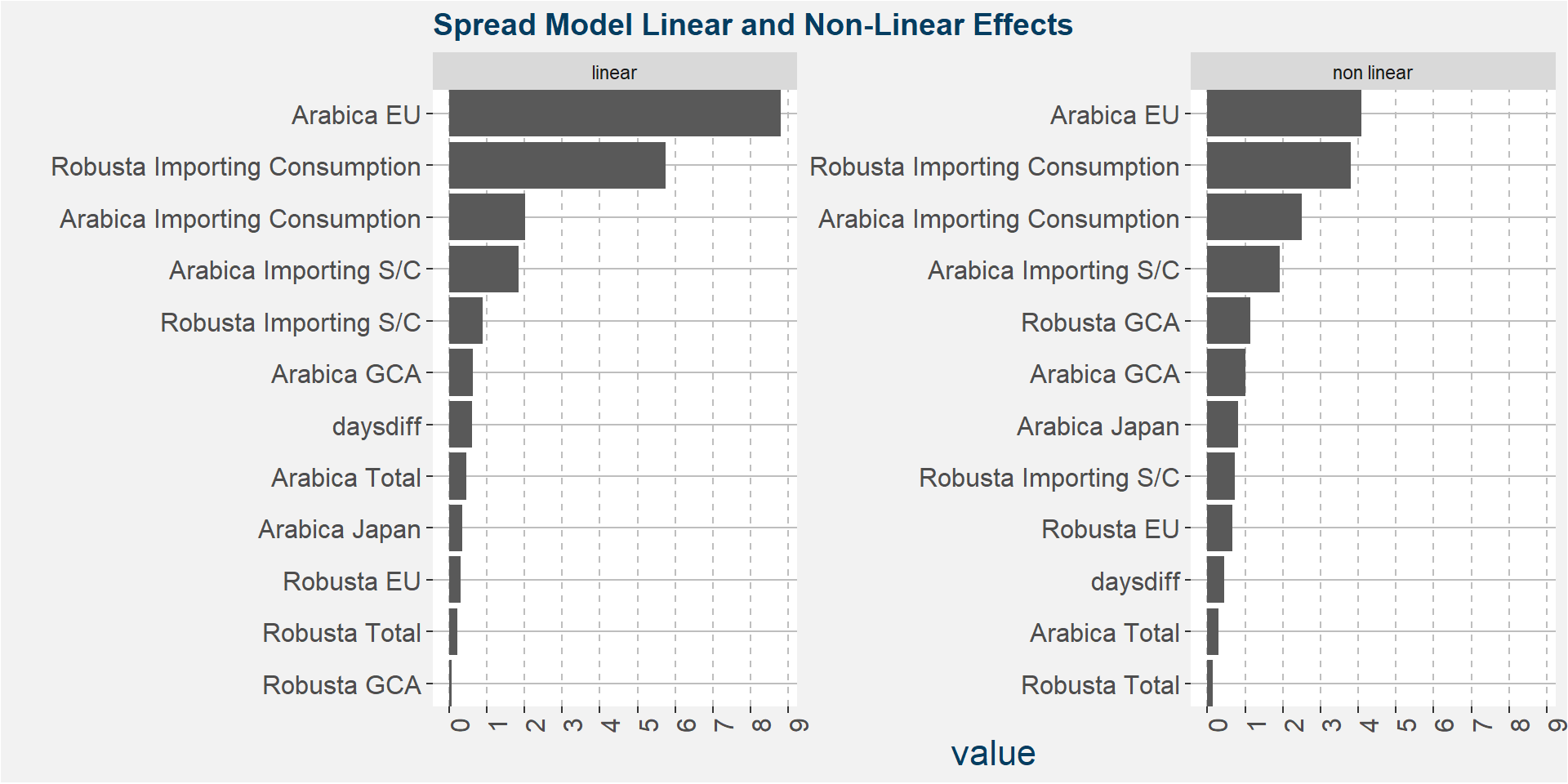
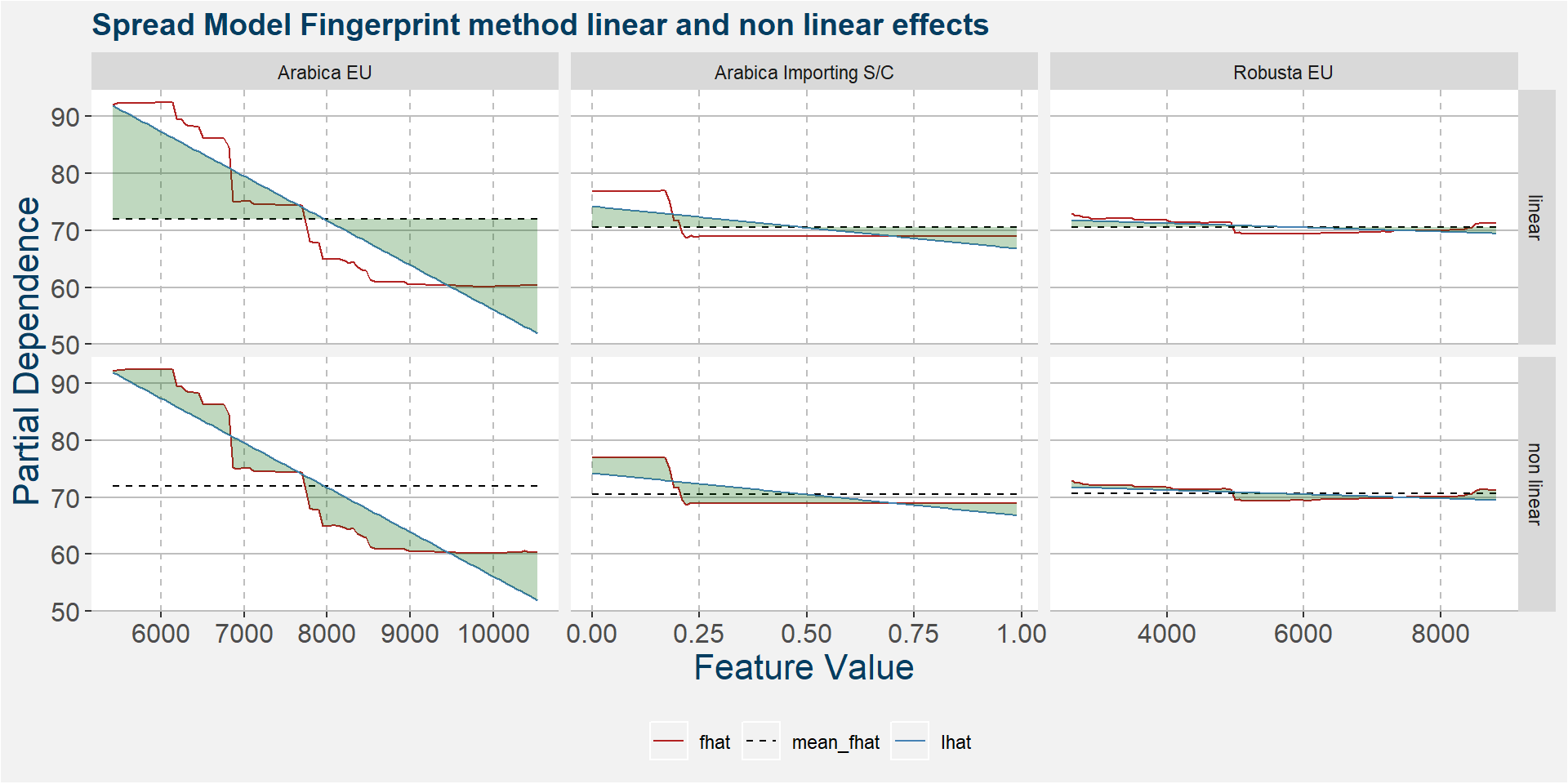
The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

N - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.55 0.58 0.91
ratio oob NA NA 0.71
ratio out of sample 0.46 0.48 0.56
spread in sample 0.63 0.63 0.93
spread oob NA NA 0.67
spread out of sample 0.39 0.39 0.71

U

U - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
U SHAP 0.461 ratio
U CFI 0.255 ratio
U MDA 0.131 ratio
U SFI 0.004 ratio
U MDI -0.071 ratio
code method weighted_tau type
U MDI 0.214 spread
U SFI 0.175 spread
U MDA 0.136 spread
U SHAP 0.123 spread

Below we show the feature importances of the top positive weighted tau methods.

U - Fingerprint Method

The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

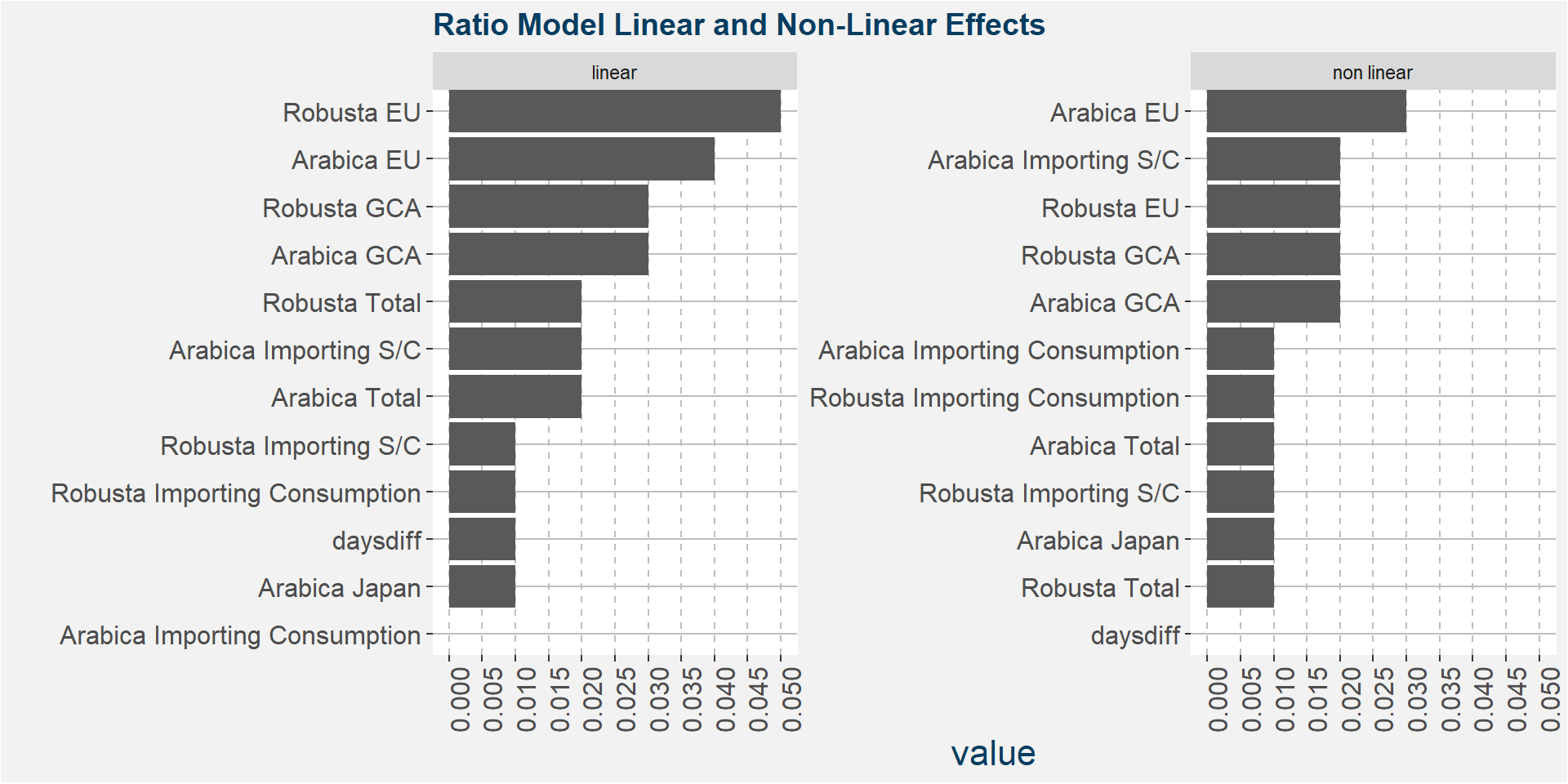
The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

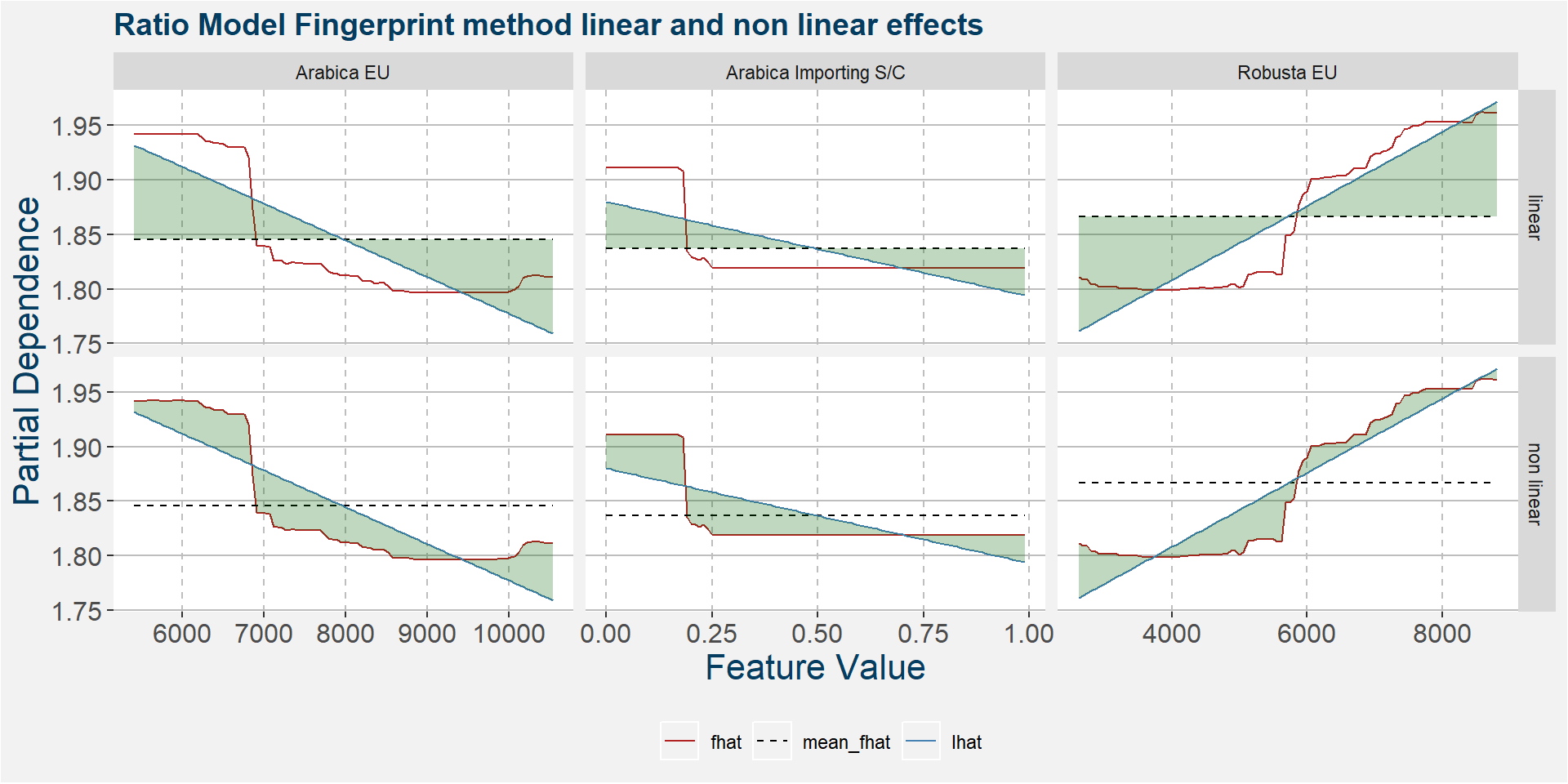
U - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.57 0.60 0.92
ratio oob NA NA 0.74
ratio out of sample 0.54 0.60 0.71
spread in sample 0.59 0.59 0.89
spread oob NA NA 0.80
spread out of sample 0.44 0.44 0.47

X

X - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
X MDA 0.329 ratio
X CFI 0.171 ratio
X SHAP 0.035 ratio
X SFI -0.034 ratio
X MDI -0.263 ratio
code method weighted_tau type
X SFI 0.198 spread
X SHAP 0.184 spread
X MDI 0.033 spread
X MDA -0.006 spread

Below we show the feature importances of the top positive weighted tau methods.

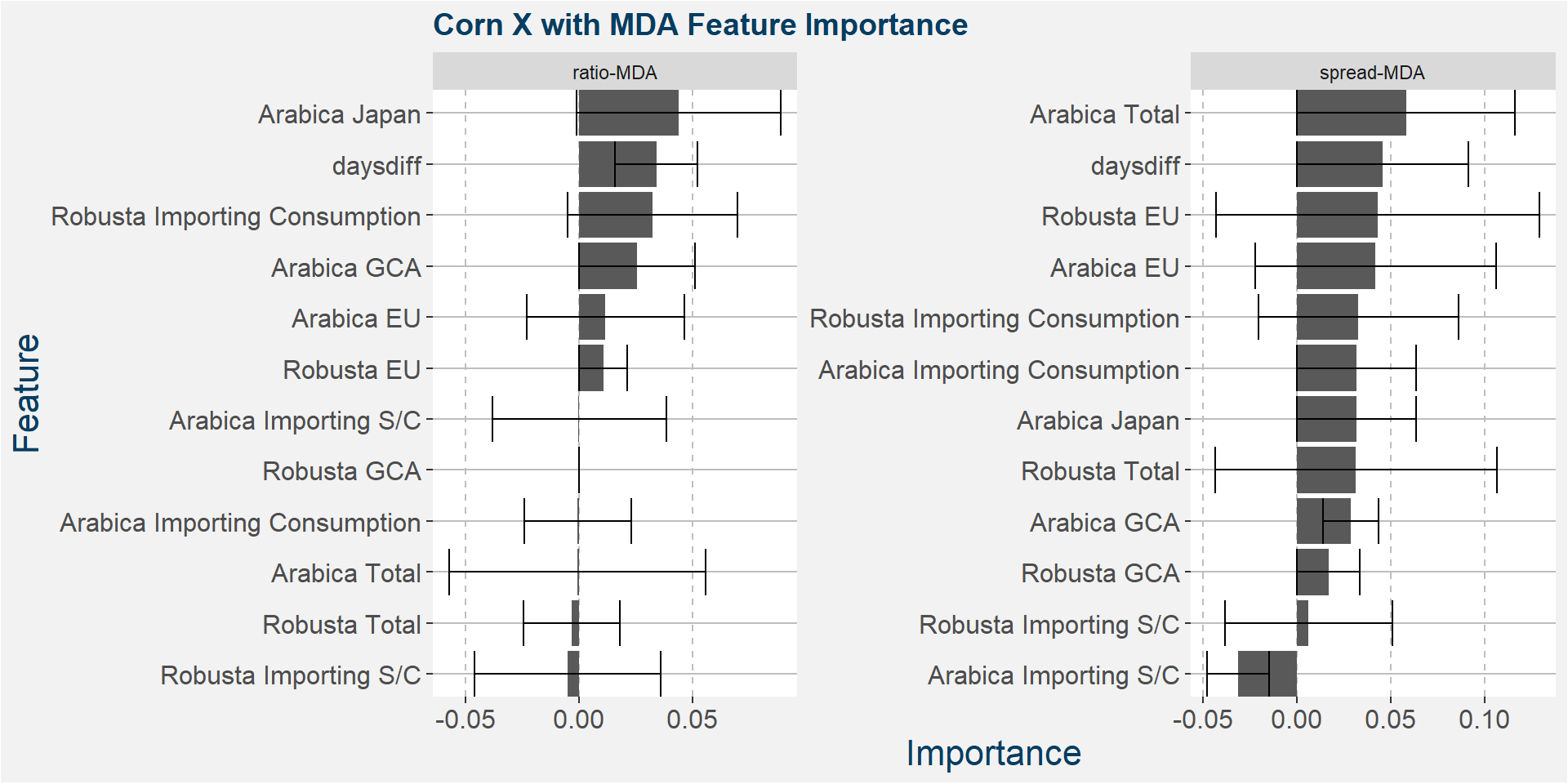
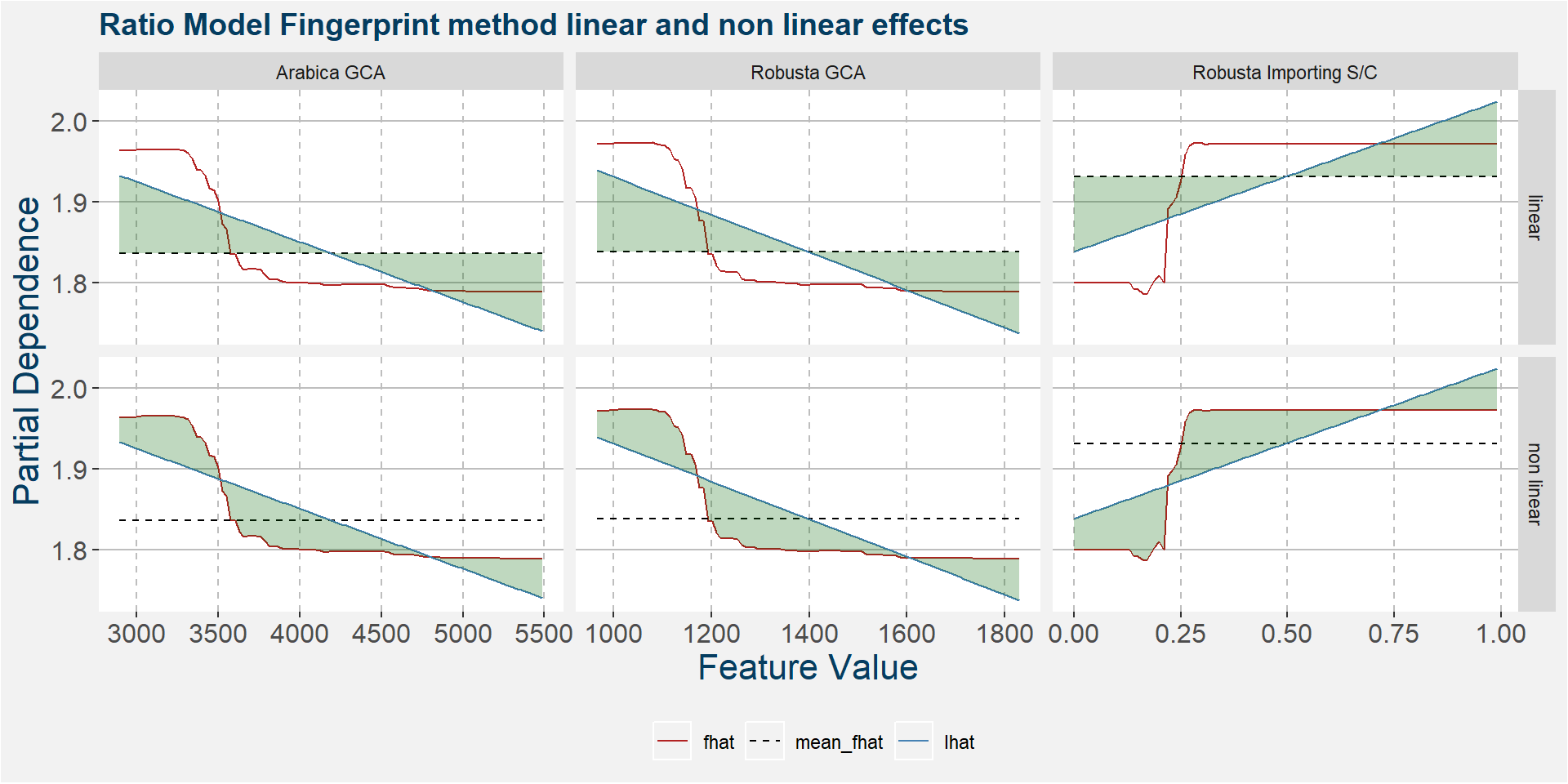
X - Fingerprint Method

The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

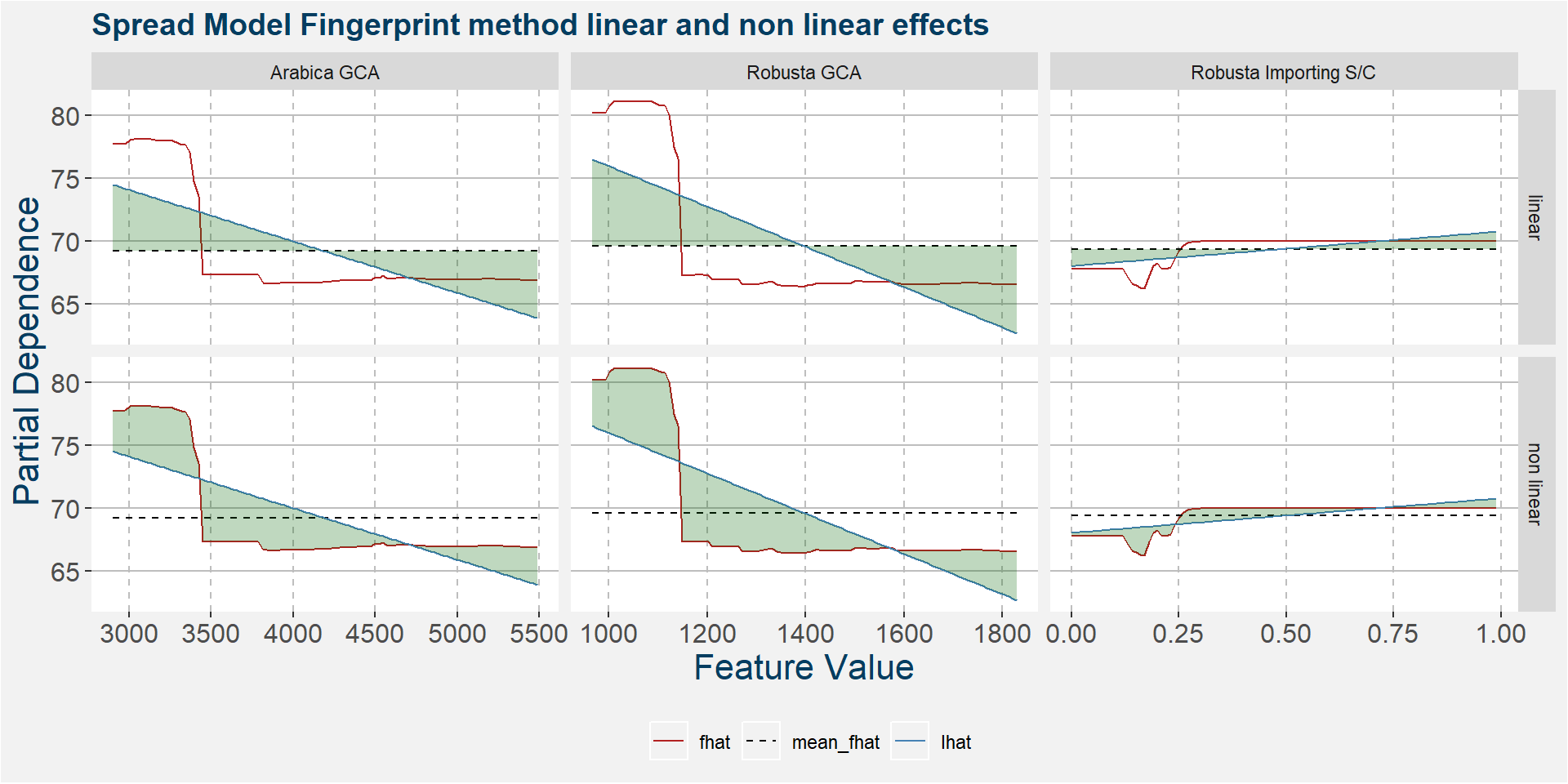
X - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.57 0.60 0.92
ratio oob NA NA 0.76
ratio out of sample 0.55 0.56 0.70
spread in sample 0.52 0.52 0.84
spread oob NA NA 0.59
spread out of sample 0.51 0.52 0.56

Z

Z - Feature Importance

The table below shows the weighted tau values of the different feature importance techniques employed.

code method weighted_tau type
Z CFI 0.255 ratio
Z SHAP 0.208 ratio
Z MDA 0.181 ratio
Z SFI 0.173 ratio
Z MDI -0.083 ratio
code method weighted_tau type
Z MDA 0.428 spread
Z SFI 0.347 spread
Z SHAP 0.117 spread
Z MDI -0.006 spread

Below we show the feature importances of the top positive weighted tau methods.

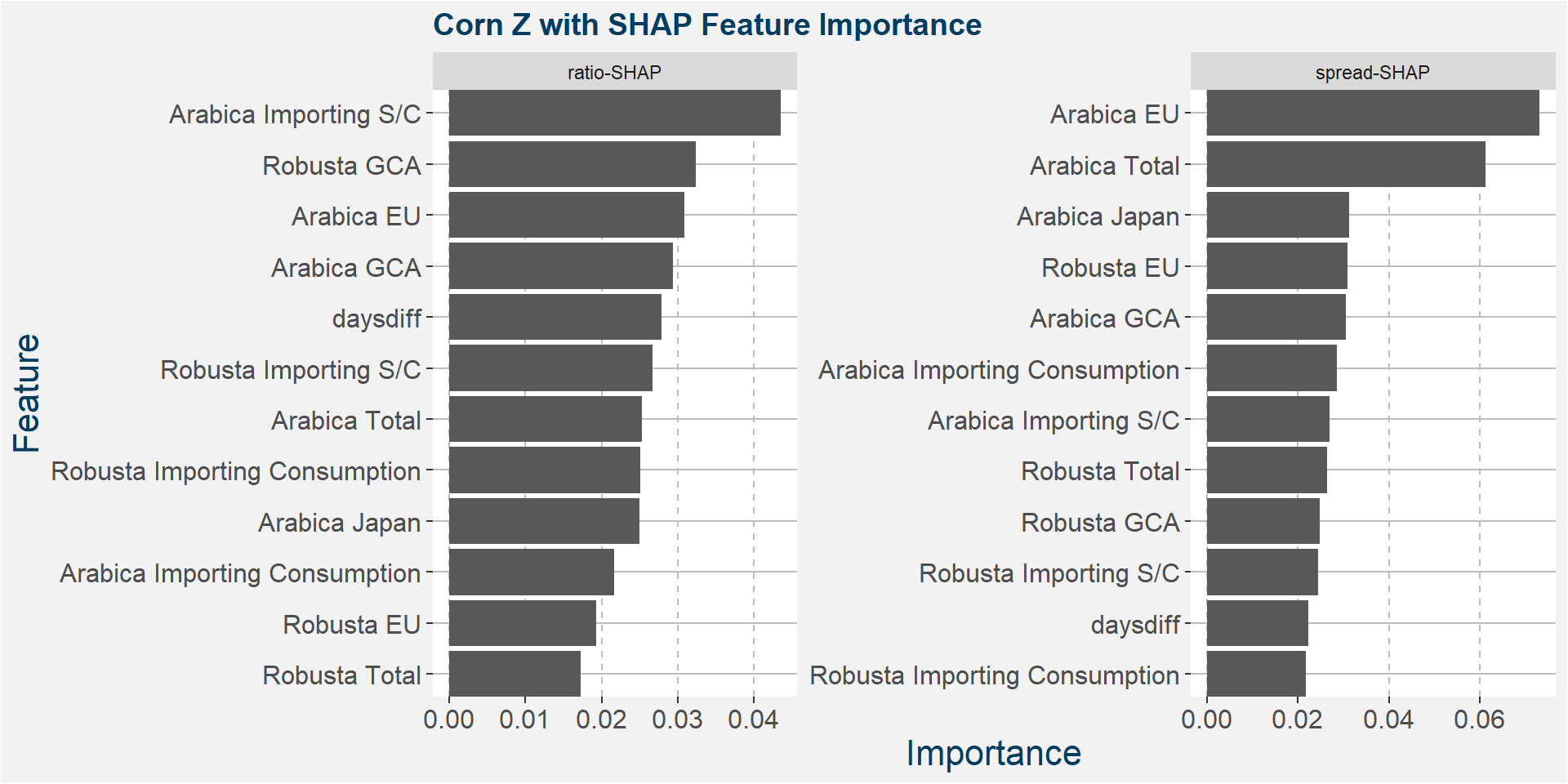
Z - Fingerprint Method

The plot below shows the normalised linear and non-linear effects in a sigle graph for easy comparison. Notice the substantial contribution from the non-linear effects.

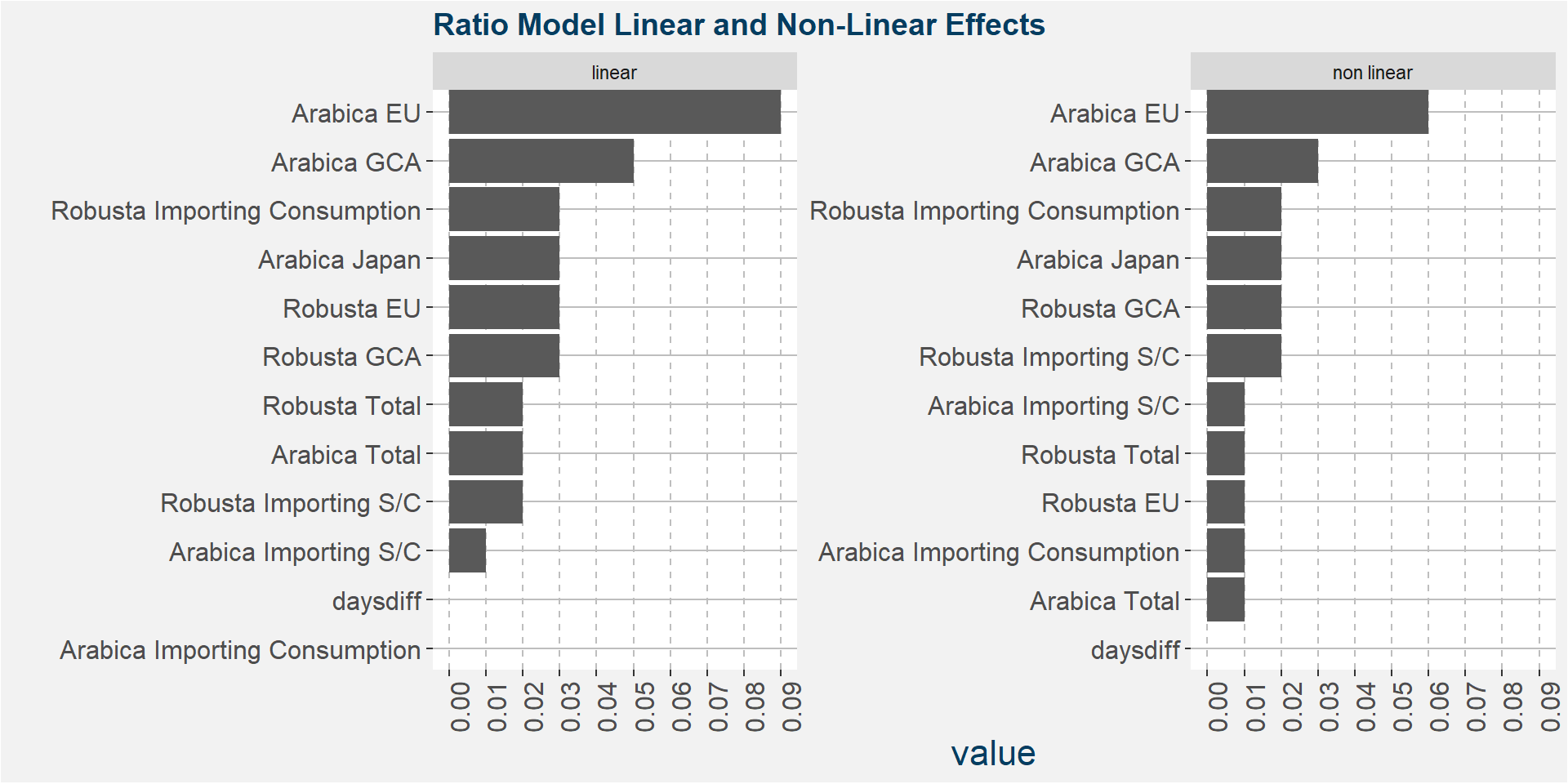
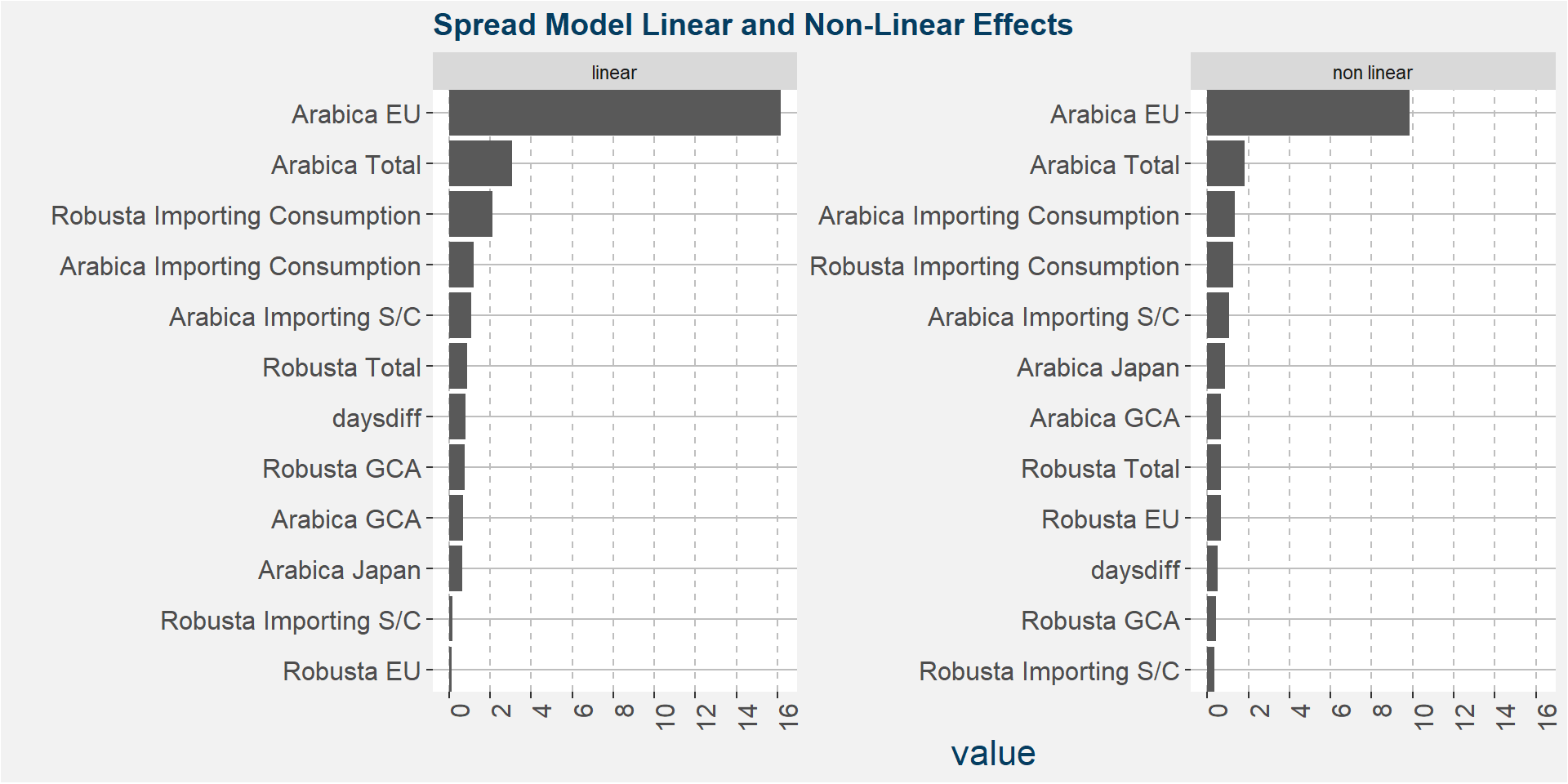
The plot below shows the linear and non linear effects as captured by the fingerprint method. These effects can be measured and compared by the shaded areas in the facet plot below. The greater the shaded area the greater the effect. The linear fit inside each facet captures the movement in the price when the feature values are changed. Elbows in the data are interesting and show that certain threshold values of the underlying feature show great variability either side of the threshold.

Z - Model Results

The tables below show the model performance data. The out of sample regression results are also much better than the linear models. The in-sample results are the same, however the Random Forest model outperforms on unseen data. A reason for this may be that the Random Forest model is better able to capture the nonlinear and interacton effects that might be present in the features.

type sample Lasso Regression Linear Regression Random Forest
ratio in sample 0.59 0.64 0.96
ratio oob NA NA 0.84
ratio out of sample 0.53 0.61 0.90
spread in sample 0.63 0.63 0.92
spread oob NA NA 0.60
spread out of sample 0.59 0.58 0.82

Conclusion

  • Throughout the random forest models perform better than their linear counterparts.
  • These models have been added to Shiny.
Feature Importance Coffee
Avatar
Mauritz van den Worm
Portfolio Manager and Quantitative Researcher

My research interests include the use of artificial intelligence in managing commodity portfolios

Related